A Nice Problem Trivialized By a Single Lemma!

(CGMO 2012) The incircle of a triangle ABC is tangent to sides AB and AC at D and E respectively, and O is the circumcenter of triangle BCI where \(I\) denotes the incenter of \(\bigtriangleup ABC\). Prove that \(\angle ODB = \angle OEC \)

$\textbf{Proof}$

We will first prove this lemma.

$\textbf{Lemma}$ Let $ABC$ be a triangle with incenter $I$ , A-excenter $I_a$, and denote the midpoint of arc $BC$ to be $L$, then points $B, I, C, I_a$ are concyclic with $L$ as the circle center.

(We will denote angle $A$ , $B$, $C$, as $\alpha, \beta,$ and $\gamma$, respectively.)

Also note that $\alpha + \beta + \gamma = 180$

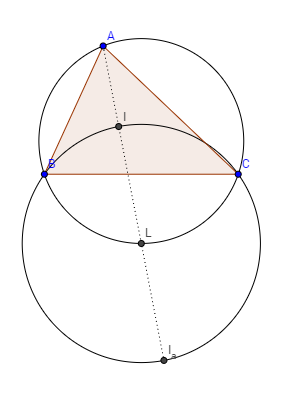
Proof: First notice that $L$ is the intersection of the angle bisector of $A$ and perpendicular bisector of $BC$.

First we prove that $LB = LI = LC$.

Since the perpendicular of $L$ to $BC$ is the perpendicular bisector of $BC$, we know that $LB = LC$.

Because $BI, AI$ are angle bisectors, we know that $\angle IAB = \frac{\alpha}{2}$ and $\angle ABI= \angle IBC = \frac{\beta}{2}$. By Exterior Angle Theorem, we know that $\angle BIL = \frac{\alpha + \beta}{2}$. If we prove that $\angle IBL = \frac{\alpha + \beta}{2}$ we have proved the segments are equal.

Notice that $\angle CBL = \angle LAC = \frac{\alpha}{2}$ because they substend the same arc. Therefore this implies that $\angle IBL = \angle IBC + \angle CBL = \frac{\alpha+\beta}{2} = \angle BIL$. Thus, by isosceles triangles we get that $LB = LI = LC$. This tells us that $B, I, C$ are concyclic with $L$ as a center.

Now, we must prove that $I_a$ also lies on this circle.

Recall that the $I_a$ is the intersection of the exterior-angle bisectors of $B$ and $C$. Therefore if you extend $AB$ and $AC$ and construct the angle bisector of the exterior angle, it intersects at $I_a$.

Denote $M$ as a point on ray $AB$ past B.

By Exterior Angle Theorem, we have that $\angle MBC = \alpha + \gamma$.

Since $BI_a$ is the angle bisector, we have that $\angle I_aBC = \frac{\alpha + \gamma }{2}$ . Since $\angle LBC = \frac{\alpha}{2}$, this implies that $\angle I_aBL = \frac{\gamma}{2}$.

We proved that $\angle LBI = \angle LIB = \frac{\alpha + \beta}{2} \implies \angle BLI = \gamma$ .

Again by exterior angle theorem, since $\angle LBI_a = \frac{\gamma}{2}$, we have that $\angle BI_aL = \frac{\gamma}{2}$ which implies that $\bigtriangleup BLI_a$ is isoscles which implies that $BL = LI_a \implies BL = LI_a = IL = LC$. Therefore $I_a$ must be concyclic with $B, I, C$ because it's radius to the center, $L$, is the same. Therefore, we have proved the lemma.

Okay good. Now let's have fun.

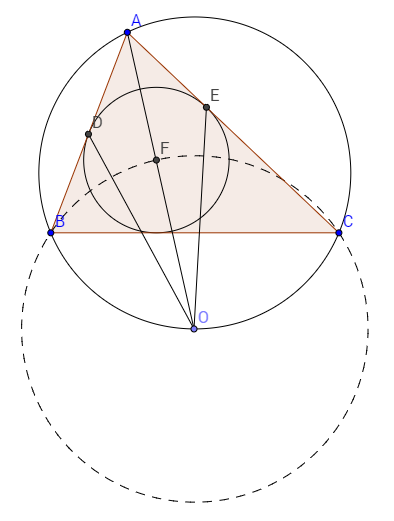
Restatement: The incircle of a triangle ABC is tangent to sides AB and AC at D and E respectively, and O is the circumcenter of triangle BCF where $F$ denotes the incenter of $\bigtriangleup ABC$. Prove that $\angle ODB = \angle OEC$

By the lemma, we know that the circumcenter, $O$, of $\bigtriangleup BFC$ is actually the midpoint of arc BC of the circumcircle of $\bigtriangleup ABC$.

To prove $\angle ODB = \angle OEC$, it suffices to prove that $\angle ADO = \angle AEO$.

Since $O$ is on the angle bisector, we know that $\angle DAO = \angle OAE$. We also know that $AD = AE$ because they are both tangents to the incircle. Additionally, $\bigtriangleup DAO$ and $\bigtriangleup AOE$ share side $AO$. Therefore, by $SAS$, we have that $\bigtriangleup ADO \cong \bigtriangleup AEO$.

This implies that $\angle ADO = \angle AEO \implies \angle ODB = \angle OEC$ and we are done.