Will this system keep falling or oscillate and stop?

I'm trying to figure out the dynamics of the system below:

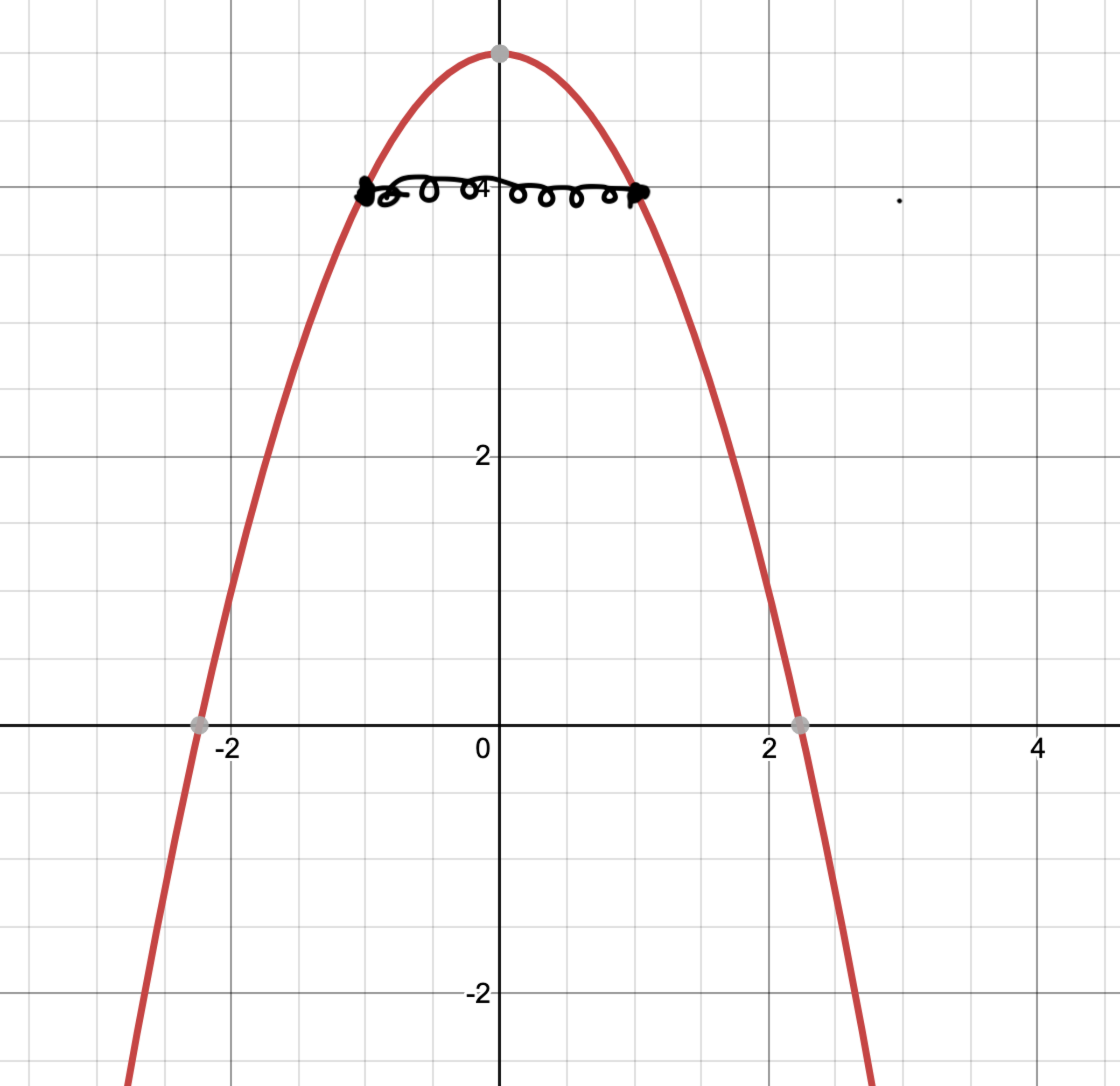
Two masses connected to an inverted parabola, free to slide. They are connected by a spring of constant $k = 20 N/m$ . Both masses are identical in every way and are of same weight ( $m = 10 kg$ ); they slide down/up the parabola at the same time.

The natural length of the spring is $l_0 = 2m$ ; gravitational acceleration $g = 10 m/s^2$ ; and the frictional coefficient of the parabola is $\mu = 0.5$ .

So, I'm trying to find out the dynamics of the system using code.

Please, if you can, provide a source code that simulates the dynamics of the system.

The physics behind the simulation:

Tangential Forces

There are 3 forces acting on the block, tangential to the ramp.

The tangential gravitational force is given by:

$\vec{\bold{F}}_{Tg} = -mg \sin(\theta) \bold{\hat{t}}$

Where $\bold{\hat{t}}$ is the unit tangent vector and $\theta$ is the angle of the tangent.

Tangential spring force can be resolved using $\theta$ ; it is given by $\vec{\bold{F}}_{Ts} = k(2x-l) \cos(\theta) \bold{\hat{t}}$ .

And then we have the frictional force which acts opposite to the movement of the mass. To calculate this we have to calculate the normal forces.

Normal Forces

There are two forces which contribute to the total normal force; gravitational and spring.

The normal force by gravitation on a ramp is given by $\displaystyle \vec{\bold{F}}_{g \bold{\hat{n}}} = mg \cos(\theta) \hat{\bold{n}}$ .

The spring part of the normal force is orthogonal to the tangent, and can also be resolved using $\theta$ :

$\displaystyle \vec{\bold{F}}_{s \bold{\hat{n}}} = k(2x-l) \sin(\theta) \hat{\bold{n}}$ .

Total Force

Once these normal forces are calculated, we can calculate the frictional force:

$\displaystyle \vec{\bold{F}}_{\mu} = \mu(\vec{\bold{F}}_{s \bold{\hat{n}}} + \vec{\bold{F}}_{g \bold{\hat{n}}}) \bold{\hat{t}}$

So, total force:

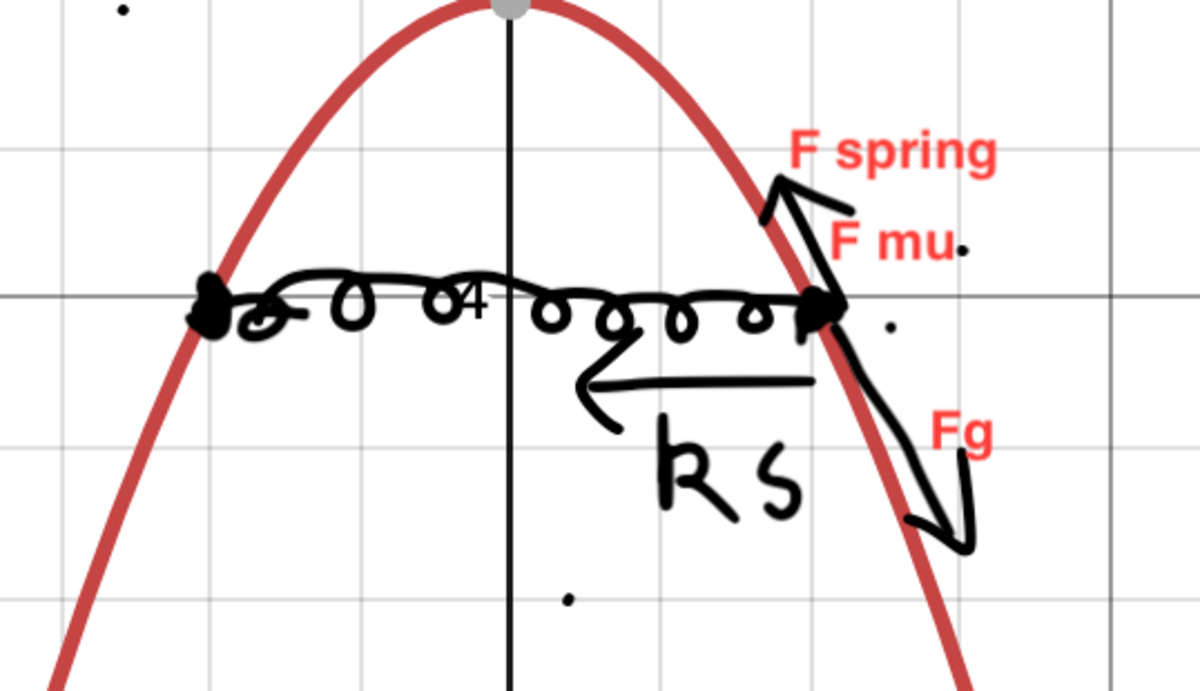
$\vec{\bold{F}}_{total} = \vec{\bold{F}}_{Ts} + \vec{\bold{F}}_{Tg} \pm \vec{\bold{F}}_{\mu}$

So guys, the main problem is that the tangential spring force is too small and the gravitational tangential force always pulls the object down and it never goes back up or undergoes oscillatory motion. The tangential ramp angle goes off to 90 degrees, which I don't think it should be doing; the spring doesn't seem to be bringing it back up. As a result of the ramp angle increasing to 90 degrees, there is almost no spring force to bring it back into oscillatory motion.

The question I would like to ask is:

Does the above system oscillate? Is the code producing a realistic result at all?

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

The spring is very beautiful.

Talulah Riley - 10 months ago

Lol yeah; drew it in class using preview on mac lmao

Krishna Karthik - 10 months ago

Ok; so what do you think about my physics/newtonian diagram? Is it correct? You don't have to look at the code if you don't want to.

I will take a closer look after some time. Thanks for sharing this. Looks interesting.

Karan Chatrath - 10 months ago

Yeah. Thanks mate :)

Did you create any simulation code for this problem? If so, please share the code with me. Thanks.

No, I have not yet attempted this. I will when I can and respond to this thread. Thanks for your patience.

@Karan Chatrath – No worries, thanks mate.

@Krishna Karthik – @Krishna Karthik, hii bro, is there any analytical way to find the area of this figure $\frac{(x+y)^{2}}{16}+\frac{(x-y)^{2}}{9}=1$

Thanks in advance.

@Talulah Riley – Hmmm... I'll take a look right away.

@Talulah Riley – Have you tried parametrising the figure? And then maybe do a line integral?

@Krishna Karthik – @Krishna Karthik I didn't know how to parametrise it?

@Talulah Riley – Are you ok with a numerical solution?

@Krishna Karthik – @Krishna Karthik No. It is a jee problem.

@Talulah Riley – Actually, I think I have a train of thought. The figure is a rotated ellipse. If we can find the equation of the original ellipse, finding the area is easy.

@Talulah Riley – Ok; I'm thinking that the major axis of the ellipse is: 2.8284

And the minor axis:

2.121

So the area is 18.85 units squared

@Talulah Riley – Ok, I've got the answer!

@Krishna Karthik – @Krishna Karthik How do you find length of major and minor axis?

@Talulah Riley – First you should find out the rotation applied on the ellipse. I've got to admit; I first graphed the function just to visualise the shape. It was then that I realised it was a rotated ellipse that got rotated anti-clockwise.

By doing some algebraic manipulation (Maybe applying a rotation matrix to it, you can find that with the equation:

$\displaystyle \frac{\left(x\cos\left(a\right)-y\sin\left(a\right)\right)^{2}}{2.828^{2}}+\frac{\left(x\sin\left(a\right)+y\cos\left(a\right)\right)^{2}}{2.121^{2}}=1$

When $\alpha = -3.8$ it provides the desired equation.

@Krishna Karthik – @Krishna Karthik after that?

@Talulah Riley – The above comment is edited. Check it out.

If you can visualise that the function is a rotated ellipse, you can use Pythagoras' Theorem like so:

Major axis: $\sqrt{1.5^2 + 1.5^2} = 2.121$

Minor axis: $\sqrt{2^2 + 2^2} = \sqrt{8} = 2.828$

There is an alternative way of finding the major and minor axis.

If you can find an expression for $\sqrt{x^2 + y^2}$ , and maximise the expression, or minimise the expression (minor axis) using calculus, you can find the major and minor axes.

When the above expression is minimum, you can find the minor axis; when the above expression is maximum, you can find the major axis.

However, either approach is hard. Are you not allowed to look at the graph of the equation? If you look at the graph of the equation, the problem gets way easier.

@Lil Doug Please let me know if you're allowed to visualise the graph of the function.

@Talulah Riley – Equation of an ellipse having points with distance from major axis $p_2$ , distance from minor axis $p_1$ , length of semi-major axis $a$ and length of semi minor axis $b$ is

$\frac{p_1^2}{a^2} + \frac{p_2^2}{b^2} = 1$

Here, $p_1 = \frac{x+y}{\sqrt2}$ and $p_2 = \frac{x-y}{\sqrt2}$ . Putting, we get

$\frac{(\frac{x+y}{\sqrt2})^2}{8} + \frac{(\frac{x-y}{\sqrt2})^2}{4.5} = 1$

So, we get $a = \sqrt{8}$ and $b = \sqrt{4.5}$ . So, area of ellipse is $\pi (\sqrt8)(\sqrt{4.5})$ .

Aryan Sanghi - 8 months, 2 weeks ago

@Aryan Sanghi – Yeah; nice substitution there. Thanks mate. I kind of cheated and used desmos lol.

Krishna Karthik - 8 months, 2 weeks ago

@Karan Chatrath

If you're free, could you maybe take a look at my newest problem, simulating dynamics 5.0? Thanks mate. Let me know if the solution's correct or not.

Krishna Karthik - 9 months, 3 weeks ago

Sorry that I did not look into the problem in this discussion. I will attempt the new problem when possible.

Karan Chatrath - 9 months, 3 weeks ago

@Karan Chatrath – No problem mate; no pressure. Take your time😁

Inspiration:

Spring on parabola (Steven Chase)

Graphical Mechanics (Aryan Sanghi)

Thanku for mentioning my problem. Your logic and code seems fine to me. @Krishna Karthik. :)

Sidenote: You could put link text in [] brackets and link address in () bracket to get a link. Example-[Spring Parabola] + (https://brilliant.org/discussions/thread/a-programming-issue-i-need-help-with-simulation/?ref_id=1600309) without + sign gives Spring Parabola

Aryan Sanghi - 10 months ago

Yeah. Thanks mate. The logic for the problem seems fine to me, but what I can't seem to trouble shoot is values shooting off to infinity in the MATLAB code. Thanks for verifying the physical correctness.

@Krishna Karthik – Maybe that arctan is causing trouble. If no, try using modular codes, i.e. take all values mod 1000000007 as it is a prime number so it will be easier to take inverse modulo. :)

@Aryan Sanghi – Hmmm. To stop the atan function to shoot off to infinity at $x = 0$ , I basically put in an if statement to handle the exception. What I find weird is that the simulation code actually shows the mass falling down forever; another weird thing is that the $\sin()$ function for the tangential spring force is actually really small; the tangential spring force is too small for it to go back up when in reality it should. I think some angles may be resolved wrong.

@Krishna Karthik – Hmm, maybe. I'll see to the code more clearly afterwards. :)

@Aryan Sanghi – Thanks for your insight bro. I will try to take your tips into account.

@Aryan Sanghi

Actually, I'm seriously doubting something. Is the above system even meant to be in oscillatory motion? Or is that just a preconceived notion that I'm having? Please let me know when you're free. Thanks bro.

Krishna Karthik - 9 months, 4 weeks ago

@Krishna Karthik – It will be a oscillatory motion as at one point, the spring will be stretched so much that it has to again return. But, if you give much initial velocity, it might happen that it will leave the parabola in its upward journey, which can be a trouble. So, you've to give a limited initial velocity. Maybe I'll post a similar question if you permit, I'll give you ye credits. @Krishna Karthik

Aryan Sanghi - 9 months, 4 weeks ago

@Aryan Sanghi – Sure bro. The simulation shows that it'll fall down once the tangential angle is too high, ie. too close to 90 degrees.

@Lil Doug

I've posted the problem in the calculus section. I hope you don't mind. Thanks bro.

To be honest, I wouldn't have solved the problem if I hadn't seen what the figure looked like.

@Krishna Karthik oh Fuck. Bro i just clicked on Dicussed solution instead on Type answer.
Please repost the problem. It will take you 1 minute only.

Sure.No problem my dude :)

Ok; it's reposted.

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$