A wonderful Proof of $A.M \geq G.M$ inequality

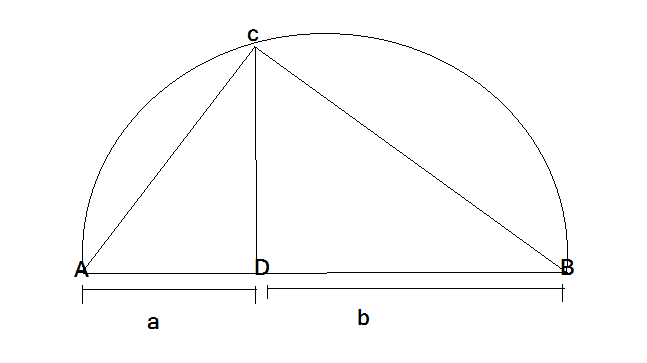
Lets us consider a semicircle with diameter AB. If C is any point on the semicircle, then ABC forms a right angled triangle with right angle at C .

Let CD be the perpendicular to AB dropped from C . Let AD= a and DB=b

The trianges DAC and DCB are similar , hence

$\frac{DA}{DC} = \frac{DC}{DB}$

therefore

$DC^{2} = DA . DB = ab$

and thus $DC = \sqrt{ab}$

if r is the radius of the semicircle , then $DC \leq r$

we know $r = \frac{diameter}{2} = \frac{a + b}{2}$

Thus

$\boxed{ \frac{a + b}{2} \geq \sqrt{ab}}$

If $DC = r$ that is if the Point D comes on the center of the circle then $a = b$

Please reshare if you liked it

#Algebra

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Geometry proves AM-GM. That's the beauty of mathematics. Reshared!

Sanjeet Raria - 6 years, 7 months ago

Great @megh choksi Keep it up bro

Deepanshu Gupta - 6 years, 7 months ago

How to mention someone on brilliant?

U Z - 6 years, 7 months ago

Just write @Name which You want to post

Deepanshu Gupta - 6 years, 7 months ago

Geometry can also prove RMS, AM, GM, HM too. Look at here.

Samuraiwarm Tsunayoshi - 6 years, 7 months ago

the only condition when DC = r will be when D is the centre of circle. And taking D as the centre of circle will it self make AD = a = radius = b = DB, why do we even need such a long calculation?

Ahmed Yaseen - 6 years, 7 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

A wonderful Proof of A.M≥G.M A.M \geq G.MA.M≥G.M inequality

Comments

A wonderful Proof of $A.M \geq G.M$ inequality