About Congruent Triangles

In school, we all learned the conditions for determining the congruence of triangles. There are usually 5 kinds of things mentioned in the textbook : $SSS,SAS,AAS,ASA,HL$. We notice that the above conditions are all around angles and edges, but there are other lines and points, such as Angle bisectors, heights, centers, etc. Can we use other conditions to determine the congruence of triangles? I made three proofs by myself. But there are too many of these to do it myself. If anyone has a great idea, let me know in the comments section and I'll add it to my note.

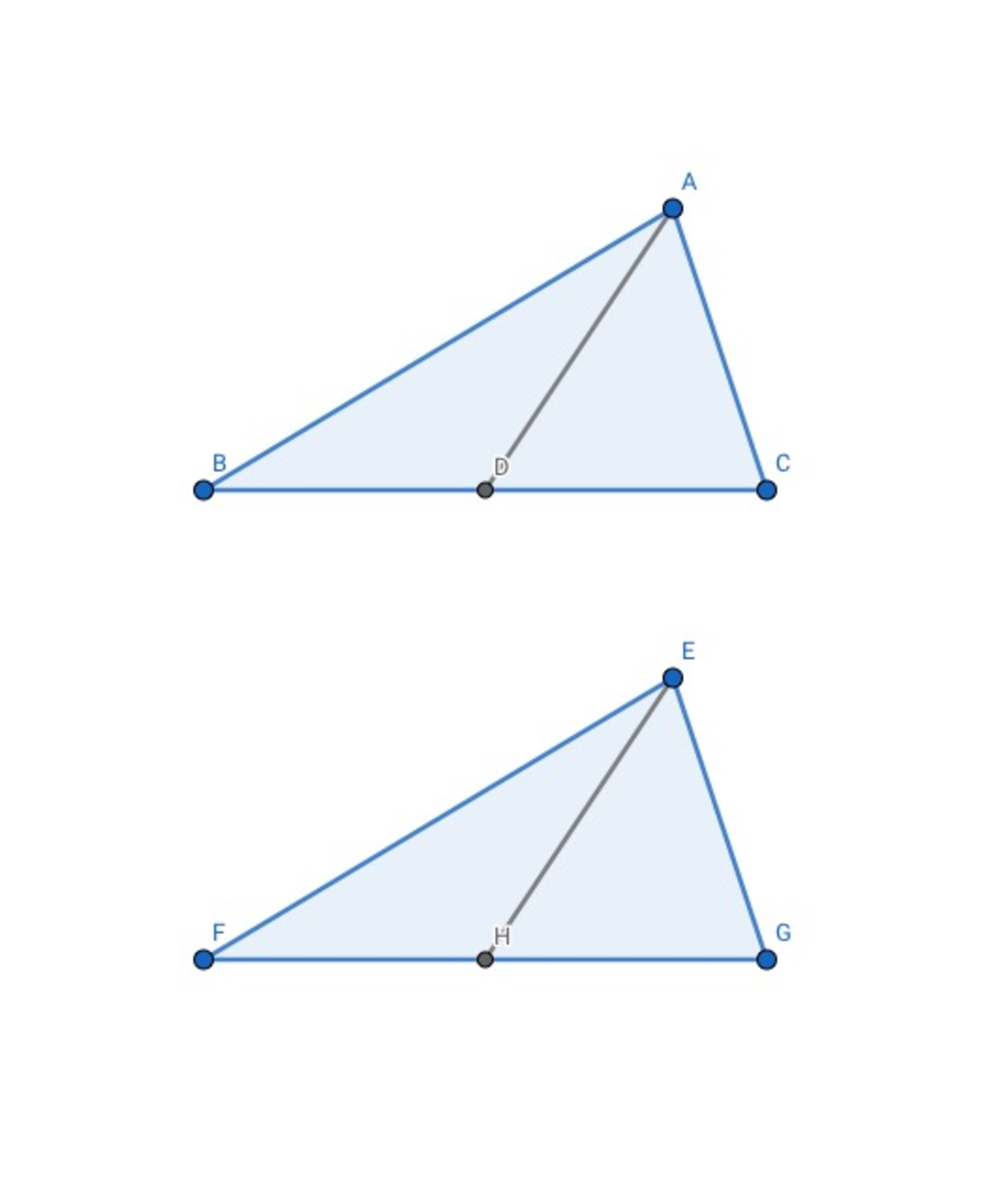
When two triangle have two equal edges and one side has an equal midian,they are congruent figures.

---

In the picture, $AC=EG$,$BC=FG$, $AD$ and $EH$ are midians on $BC$ and $FG$.

$\because D$ and $H$ are midpoint on $BC$ and $FG$, there are $BC=FG$. $\implies CD=GH,BD=FH$.

In the $\triangle ACD$ and $\triangle EGH$, $AD=EH,AC=EG,GH=CD$

$\therefore \triangle ACD \cong \triangle EGH(SSS)\implies\angle ACB=\angle EGF$

In the $\triangle ABC$ and $\triangle EFG$, $AC=EG,\angle ACB=\angle EGF,BC=FG$

$\therefore \triangle ABC\cong \triangle EFG(SAS)$

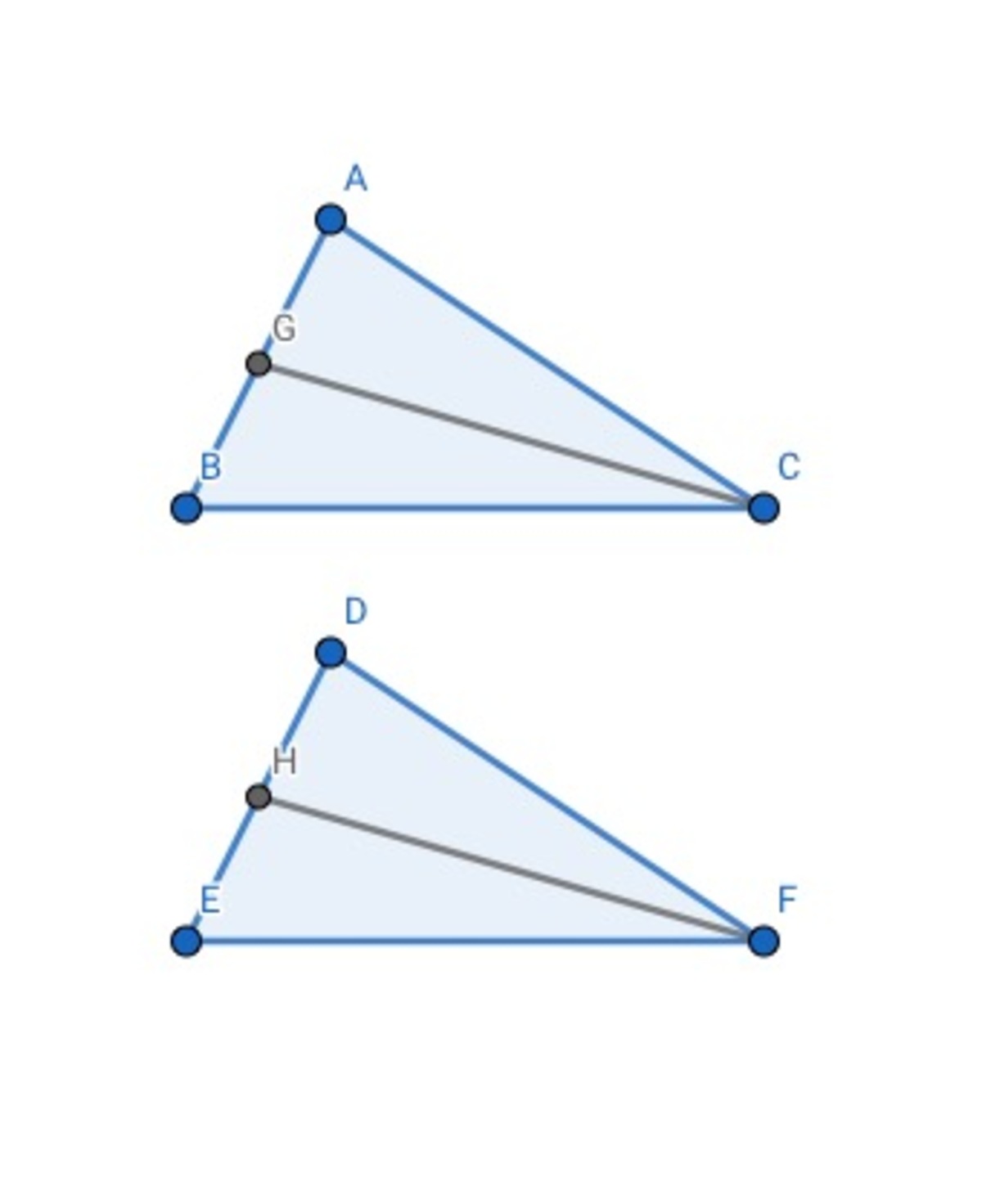
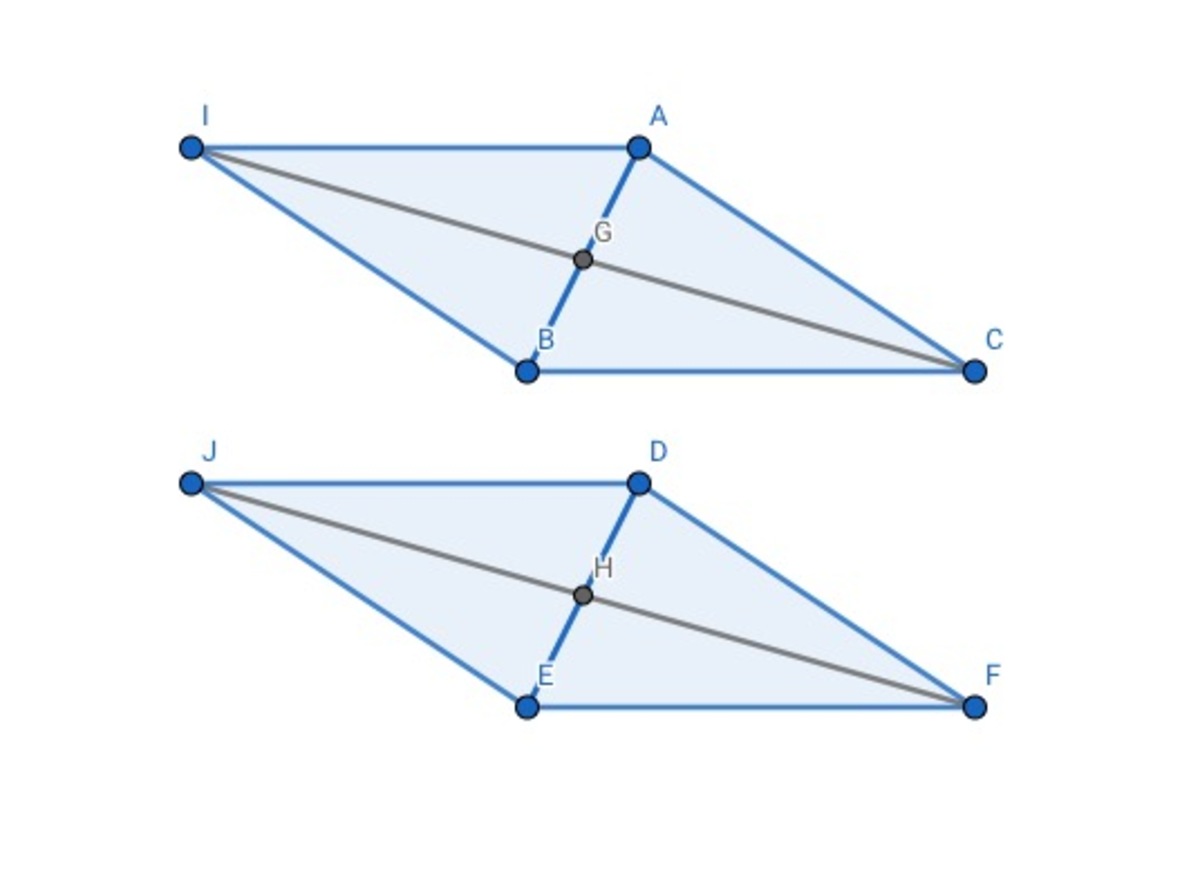
When two triangles have two equal edges and the other side has an equal midian, they are congruent figures.

---

In the picture, $AC=DF$, $BC=EF$, $CG$ and $FH$ are midians on $AB$ and $DE$

We extend $CG$ and $FH$ to $I$ and $J$, and let $CG=IJ=\dfrac12 CI, FH=JH=\dfrac12 FJ$.

$\implies G$ and $H$ are midpoints on $CI$ and $FG$. Also, $G$ and $H$ are midpoint on $AB$ and $DE$.

$\implies AIBC$ and $DJEF$ are parallelograms. $\implies AC=BI, DF=EJ\implies BI=EJ$

$\because AC=DF, BC=EF, CG=FH \implies 2CG=2FH \implies CI=FJ$

In the $\triangle BCI$ and $\triangle EFJ$, $BC=EF, CI=FJ, BI=EJ$

$\therefore \triangle BCI \cong \triangle EFJ(SSS) \implies \angle EFJ=\angle BCI$

Also, we can know $\triangle ACI\cong \triangle DFJ(SSS) \implies \angle ACI=\angle DFJ$

$\therefore \angle ACI+\angle BCI=\angle DFJ+\angle EFJ\implies \angle ACB=\angle DFE$

In the $\triangle ABC$ and $\triangle DEF$,$AC=DF, \angle ACB=\angle DFE, BC=EF$

$\therefore \triangle ABC\cong \triangle DEF(SAS)$

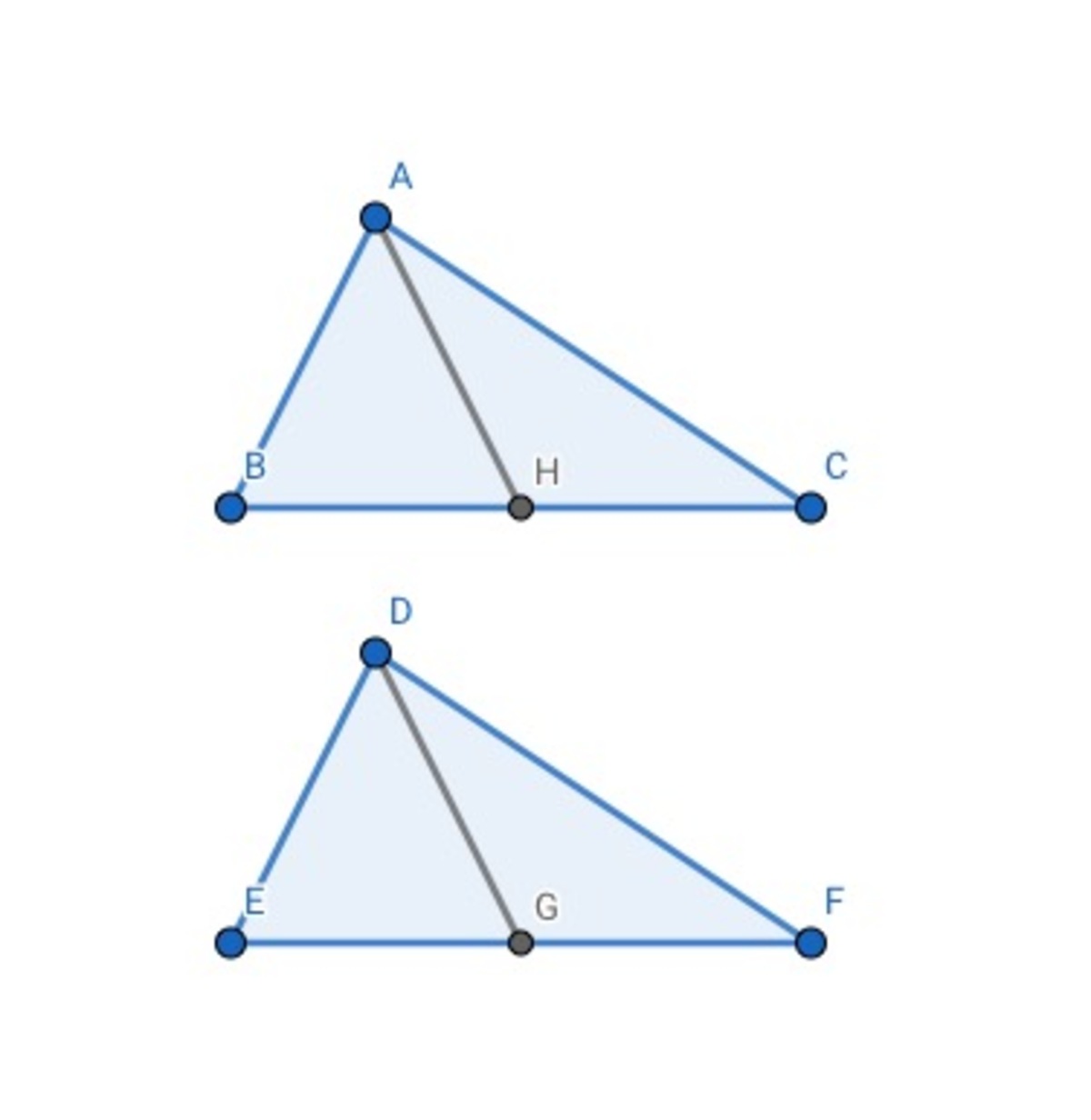
When two triangles have two equal angles and they clip edge has an equal midian, they're congruent figures.

---

In the picture, $\angle B=\angle E, \angle C=\angle F,AH$ and $DG$ are midians on $BC$ and $EF$

In the $\triangle ABC$ and $\triangle DEF$, $\angle B=\angle E, \angle C=\angle F$

$\therefore \triangle ABC \sim \triangle DEF (AA) \implies \dfrac{AC}{DF}=\dfrac{AB}{DE}=\dfrac{BC}{EF}$

$\because AH=DG \implies \dfrac{AH}{DG}=\dfrac{BC}{EF}=1 \implies BC=EF$

In the $\triangle ABC$ and $\triangle DEF$, $\angle B=\angle E, \angle C=\angle F, BC=EF$

$\therefore \triangle ABC\cong \triangle DEF(ASA)$