Absolute Value

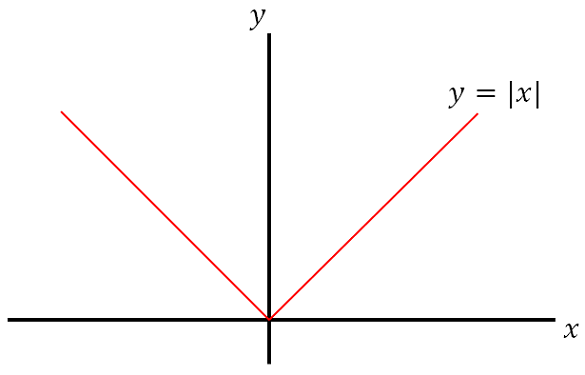
For a real number, the absolute value of \(x\), denoted \( \lvert x \rvert \), is defined as

$\left|x \right| = \begin{cases} x, & \text{if } x \geq 0 \\ -x, & \text{if } x < 0. \end{cases}$

Here are some properties of the absolute value:

1. Non-negative: $\vert x \rvert \geq 0$ for all real values.

2. $\lvert x \rvert = \sqrt{ x^2 }$ and $\lvert x \rvert^2 = x^2$ for all real values.

3. Multiplicative: $\lvert xy \rvert = \lvert x \rvert \cdot \lvert y \rvert$.

4. Sub-additive: $\lvert x+y \rvert \leq \lvert x \rvert + \lvert y \rvert$.

5. Symmetry: $\lvert -x \rvert = \lvert x \rvert$.

6. Distance to origin: $\lvert x \rvert$ measures the geometric distance of the real number $x$ to the origin $0$. Since distance is always positive, the absolute value of a number is always positive. Thinking of absolute value as the distance from zero is also helpful when considering complex numbers $z = a + bi$. This distance from $z$ to the origin is given by the distance formula: $\text{distance}_{(a,b)\leftrightarrow(0,0)} = \sqrt{(a-0)^2 + (b-0)^2}$ In fact, this is also the definition of the absolute value for a complex number $z = a+bi$:

$\left| z \right| = \sqrt{a^2 + b^2}$

Worked Examples

1. Find all real values $x$ satisfying $\lvert x - 3 \rvert = 5$.

Solution 1: If $x-3 \geq 0$, then we need to solve $x-3 = 5$, which gives $x = 8$. This satisfies the original condition of $x - 3 \geq 0$, hence is a valid solution. If $x-3 < 0$, then we need to solve $-(x-3) = 5$, which gives $-x+3 = 5$ or $x = -2$. This satisfies the original condition of $x-3 < 0$, hence is a valid solution.

Solution 2: Using property 2, we obtain $(x-3)^2 = \lvert x-3\rvert ^2 = 5^2$, or $x^2 - 6x + 9 = 25$, which reduces to $0 = x^2 -6x - 16 = (x-8)(x+2)$. This has solutions $x=8, -2$. We can verify that both of these are solutions.

2. How many real values $x$ satisfy $\lvert x^2 -1 \rvert = \lvert x-2 \rvert$?

Solution: Let's approach this problem by considering the different regions. We have $x^2 -1 \geq 0 \Leftrightarrow x\leq -1, x \geq 1$. Also, $x -2 \geq 0 \Leftrightarrow x \geq 2$.

If $x \leq -1$ then we have $x^2 -1 = 2 - x$, or $x^2 + x - 3 = 0$. This has roots $\frac{-1 \pm \sqrt{ 1^2 - 4 \times 1 \times (-3) }} {2}$, of which only the choice of $-$ satisfies $x < -1$. There is one solution in this case.

If $-1 \leq x \leq 1$, then we have $1 - x^2 = 2 - x$, or $x^2 -x + 1 = 0$. This has roots $\frac { 1 \pm \sqrt{ 1^2 - 4 \times 1 \times 1 } } {2}$ which are not real. Hence, there are no solutions in this case.

If $1 \leq x \leq 2$, then we have $x^2 -1 = 2 - x$, or $x^2 + x - 3 = 0$. We check that the root $\frac{ -1 + \sqrt{13} } { 2}$ is within this domain. Hence, there is one solution in this case.

If $2 \leq x$, then we have $x^2-1 = x - 2$, or $x^2 - x + 1 = 0$. This has no real root.

Hence, there are two real values $x$ which satisfy $\vert x^2 -1 \rvert = \lvert x-2 \rvert$.

3. Prove the sub-additive property:

$\lvert x+y \rvert \leq \lvert x \rvert + \lvert y \rvert.$

Solution 1: We apply the triangle inequality to the triangle with vertices $O = 0$, $A = x$, $B = -y$ on the real number line. Then $AB \leq OA + OB$, implying $\lvert x - (-y) \rvert \leq \lvert x \rvert + \lvert y \rvert$.

Solution 2:

If $x, y \geq 0$, then $\lvert x+y \rvert = x+y, \lvert x \rvert + \lvert y \rvert = x + y$, so $\lvert x+y \rvert \leq \lvert x \rvert + \lvert y \rvert$.

If $x, y \leq 0$, then $\lvert x+y \rvert = -x -y, \lvert x \rvert = -x, \lvert y \rvert = - y$, so $\lvert x+y \rvert \leq \lvert x \rvert + \lvert y \rvert$.

If $x \geq -y \geq 0$, then $\lvert x+y \rvert = x+y, \lvert x \rvert = x, \lvert y \rvert = -y$ so $\lvert x+y \rvert = x+y \leq x -y = \lvert x \rvert + \lvert y \rvert$. Likewise, if $y \geq -x \geq 0$.

If $x \leq -y \leq 0$, then $\lvert x+y \rvert = -x - y , \lvert x \rvert = -x, \lvert y \rvert = y$, so $\lvert x+y \rvert = -x - y \leq -x + y = \lvert x \rvert + \lvert y \rvert$. Likewise, if $y \leq x \leq 0$.

For more problems, see the Technique Trainer.