An Elegant Solution to a Complex Problem

Before trying to solve the problem I present here in this note, please make sure that you have read the complete note clearly.

Problem. Prove \[2i\tan^{-1} \left(\frac{ia}{b}\right) = \log \left|\frac{a-b}{a+b}\right|\] where $i = \sqrt{-1}$ and $a,b \in \mathbb{R}$ such that $a \neq \pm b$

Proof. Ofcoure, you can prove it in a several ways, like simplifying using complex analysis or using series expansion or maybe some other method(s).

But I'll share another elegant solution to the above problem.

Consider the following integral

$\int_0^x \frac{1}{x^2-a^2} \mathrm{d}x = \frac{1}{2a}\int_0^x \frac{1}{x-a} - \frac{1}{x+a} \mathrm{d}x = \frac{1}{2a} \log \left|\frac{x-a}{x+a}\right|$

We can also evaluate the above integral as $\int_0^x \frac{1}{x^2-a^2} \mathrm{d}x = \int_0^x \frac{1}{x^2+(ia)^2} \mathrm{d}x = \frac{i}{a}\tan^{-1} \left(\frac{ix}{a}\right)$

Thus, $\frac{i}{a} \tan^{-1} \left(\frac{ix}{a}\right) = \frac{1}{2a} \log \left|\frac{x-a}{x+a}\right|$ $\Rightarrow 2i \tan^{-1} \left(\frac{ix}{a}\right) = \log \left|\frac{x-a}{x+a}\right| \qquad \qquad \qquad \square$

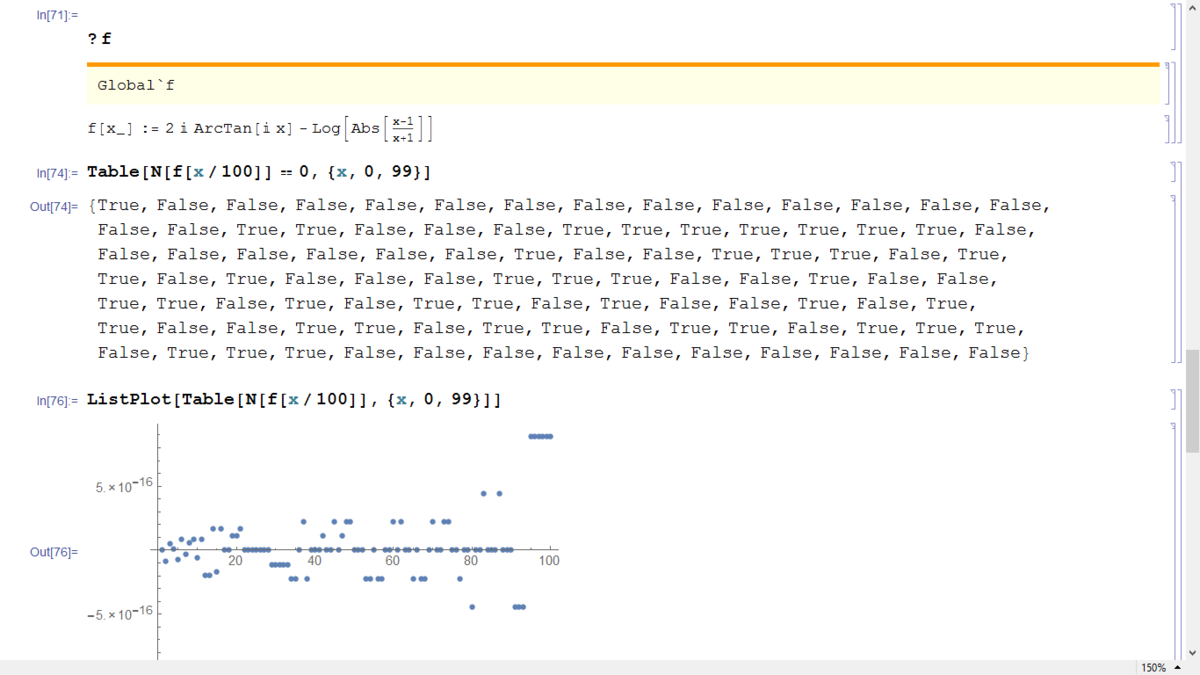
Now, here I have a problem. When I tried to verify the above result on Mathematica, it gives me the negative result. Here's a screenshot of my code (in particular, I did it for $a=1$ and for $|x| <1$ ). I expected Mathematica to return true for all values.

Can somebody help me, where am I going wrong. Is there a flaw in the result that I have proven , or is my Mathematica code wrong?

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

i solved the problem in the exact manner ! it was in Arihant level 2 complex problems right?

I too solved it through integration and later i realised that using demoures theorem (means $e^{ix}$ was much easier ,

Mvs Saketh - 6 years, 3 months ago

I derived this integral in some boring class and thought it was something great. Then I found out that using $e^{i\theta}$ , this thing is very elementary.

Raghav Vaidyanathan - 6 years, 3 months ago

@Mvs Saketh @Raghav Vaidyanathan But did you notice the last line of the note.

Mathematica doesn't gives this result, can you tell me the flaw in my code?

Kishlaya Jaiswal - 6 years, 3 months ago

I'm sorry, I do not know mathematica. But I do know that wolfram if not error free. Your result seems correct to me, but I am not able to see why you are getting false values.

@Raghav Vaidyanathan – See my comment for an explanation.

Agnishom Chattopadhyay - 6 years, 3 months ago

@Raghav Vaidyanathan – Yep, @Agnishom Chattopadhyay has already resolved the error. (Read our conversation below)

The fallacy is in the definite integrals.

In a similar way, one could prove that sin^2(x) = -cos^2(x)

$\int^x_0{\sin x \cos x \, dx} = \int^x_0{(\sin x) d(\sin x) } = \frac{1}{2} \sin^2 x$

$\int^x_0{\sin x \cos x \, dx} = \int^x_0{-(\cos x) d(\cos x) } = -\frac{1}{2} \cos^2 x$

$\implies \sin^2 x = - \cos^2 x$

Actually your last integral is incorrect. Let me explain

$\int_0^x \sin x \cos x dx = \int_0^1 -(\cos x)d(\cos x) = -\frac{1}{2}\left(\cos^2 x\right|_0^x = -\frac{1}{2}\left(\cos^2 x - 1\right) = \frac{1}{2}(1-\cos^2 x) = \frac{1}{2} \sin^2 x$

Haha, I know that already.

Sorry to confuse you, I don't think the problem is with the integral.

The problem is with the N function. Because it forces the software to convert both sides to numeric expressions, it is unlikely that they'll be the same.

I am not exactly sure why it happens but something like this might happen: Mathematica's calculation of one side may converge faster than the other. For example, if both sides are $\sqrt{2}$ , one might converge to 1.41 and another to 1.414 after a certain number of iterations.

In computation, many a times a 0 and a small 'weed' error are often indistinguishable.

To make sure what I am talking about is not crap, run the following:

f[x_] := 2 I ArcTan[(I x)/1];
g[x_] := Log[Abs[(x - 1)/(x + 1)]];

Table[f[x/100] - g[x/100] // N, {x, 0, 99}]

See how small the values are?

Okay, let us resort to symbolic computation!

1
2
3

f[x_] := 2 I ArcTan[(I x)/1];
g[x_] := Log[Abs[(x - 1)/(x + 1)]];
Table[f[x/100] - g[x/100] == 0 // FullSimplify, {x, 0, 99}]

Run the code! Does it satisfy you?

@Agnishom Chattopadhyay – Oh,yeah, now I see my flaw. Thanks

And also,

1	`Solve[2IArcTan[(*x)/1] - Log[Abs[(x - 1)/(x + 1)]] == 0,x]`

gives me all real solutions.

A great thanks to you for pointing it out. $\ddot \smile$

@Kishlaya Jaiswal – You are Welcome. :)

Actually, there shouldn't be a fallacy because I found that both the sides of expression have same series expansion.

Also, if still there is fallacy, then can you please pin-point the wrong step.

And please do share the fallacy which proves that $\sin^2x = \cos^2x$

I'm not sure of the exact fallacy but check the last comment again :)

With regards to your fallacy, that's not what you want. What you intended is

$\int \sin x \cos x \, dx = \int \sin x \, d \sin x = \frac{1}{2} \sin ^ 2 x$
$\int \sin x \cos x \, dx = \int - \cos x \, d \cos x = - \frac{1}{2} \cos ^ 2 x$

Hence, this would lead someone to claim that $\sin^2 x = - \cos ^2 x$ .

This is a common example used to represent this mistake, which is that $\int f \, dx = F(x) + C$ , as opposed to $\int f\, dx = F(x)$ . This appears numerous times, even on Brilliant. E.g. we've had to delete a lot of questions that say " Evaluate $\int f\, dx$ at $x = 0$ ", because they didn't make sense due to the $+ C$ which was forgotten.

Do you see how the mistake comes into play here?

Calvin Lin Staff - 6 years, 3 months ago

Yep, the constant is -1/2 ;)

@bobbym none I'd like you to throw some light on this

Mr Chattopadhyay; Your later comments are on the right track. You should follow a discussion that phrontister and I had a long time ago...

bobbym none - 6 years, 3 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$