Here's a proof of the identity $1^{2} + 2^{2} + 3^{2} + . . . + n^{2} = \frac{n(n+1)(2n+1)}{6}$

Geometric Intuition

Think of it as stacking squares on top of each other to make a staircase/pyramid. Here's what the cross section looks like:

Each layer is a horizontal cross section of that staircase. Our goal is to find a formula to sum up all of the balls.

In our case of $n = 4$, we can sum it up like this:

There are seven balls on the "first step" of our first layer. Here's what I mean:

That's (1) times (7) = 7 balls

Now, for the "second step" in our staircase, we have to take into consideration the balls from the base layer and the layer above that.

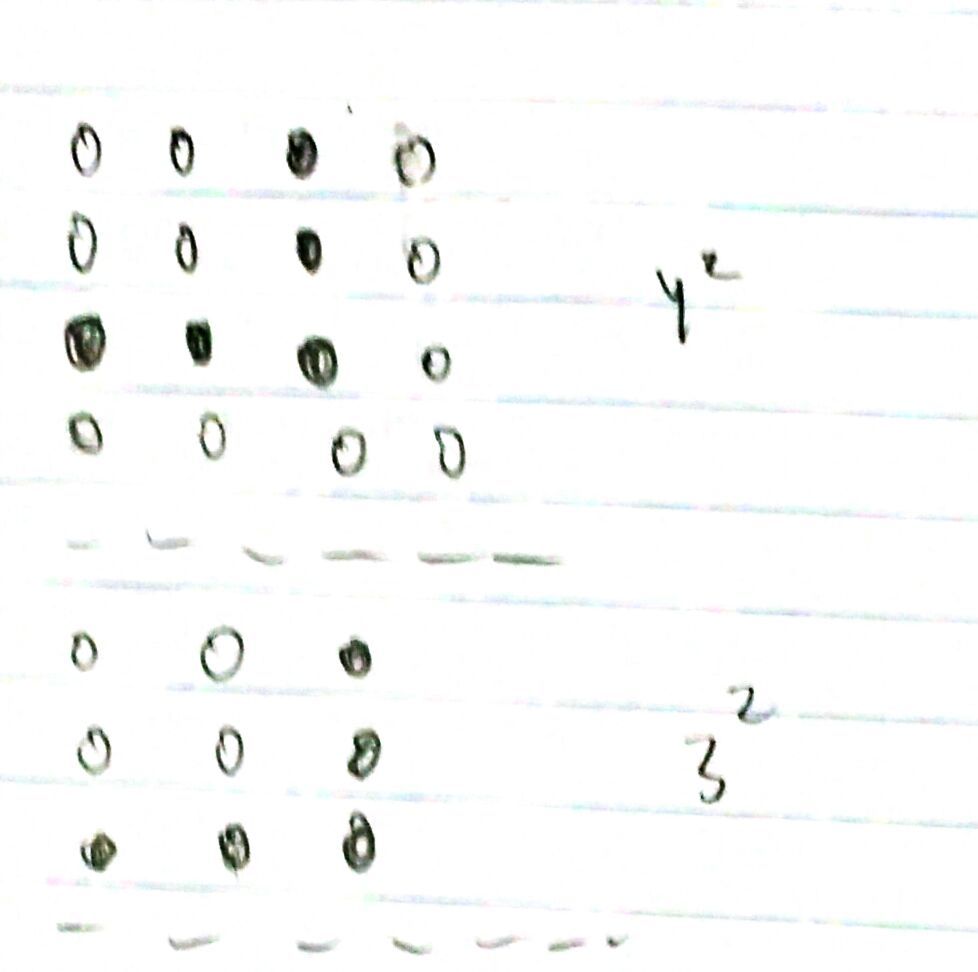
Now that's (2) times (5) = 10 balls

For the third step, we have to take into consideration the balls from the first, second and third layer.

That's (3) times (3)

The full sum looks like this: $(1)(7) + (2)(5) + (3)(3) + (4)(1)$

If you plug in 4 to the formula, it agrees with this sum, which is $\boxed{30}$.

Now we see a pattern.

For the first term, it's $1 \cdot (2(4) - 1)$

For the second term, it's $2 \cdot (2(4) - 3)$

For the $i$th term, it's $(i)(2n - 2i+1)$

Play around with it and plug some numbers in, and you will see that this is the case.

This agrees with the theorem that the sum of consecutive odd numbers is a perfect square. Here's a diagram to refresh your memory:

Algebraic Manipulation

We have

$\displaystyle \sum_{k=1}^{n} k^2 = (1)(2n - 1) + (2)(2n - 3) + (3)(2n - 5) . . . (n)(1)$

which can be represented as

$\displaystyle \sum_{k=1}^{n} k^2 = \sum_{k=1}^{n} (k)(2n - 2k + 1)$

Algebra magic

$\displaystyle \sum_{k=1}^{n} (2nk - 2k^2 + k) = \displaystyle \sum_{k=1}^{n} k^2$

$3\displaystyle \sum_{k=1}^{n} k^2 = \displaystyle \sum_{k=1}^{n} (2nk + k)$

We know that $\boxed{\displaystyle \sum_{k=1}^{n} = \frac{n(n+1)}{2}}$

$3\displaystyle \sum_{k=1}^{n} k^2 = \frac{2n \cdot n(n+1)}{2} + \frac{n(n+1)}{2}$

Therefore:

$\displaystyle \sum_{k=1}^{n} k^2 = \frac{(2n+1)n(n+1)}{6} = \frac{n(n+1)(2n+1)}{6}$

QED :-)