Analysis page (Most common Number of prime factors)

All the analysis made from the outputs of participants will be shown here.

Graph of Prime factor distribution from $0$ to $10^6$ :
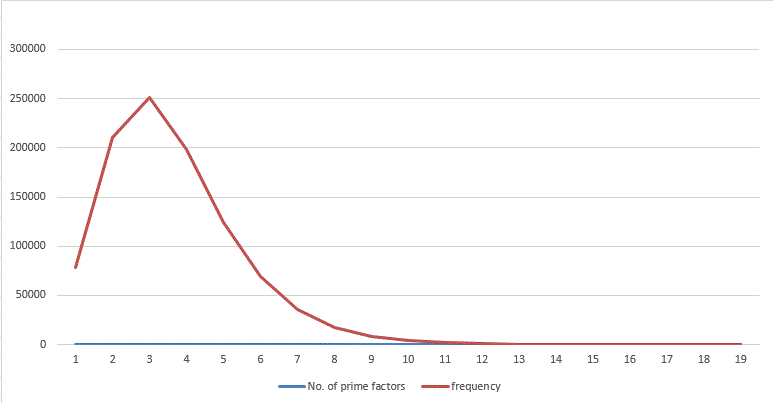
Graph of Number of prime factors occurrence percentage (till $10^6$ ):
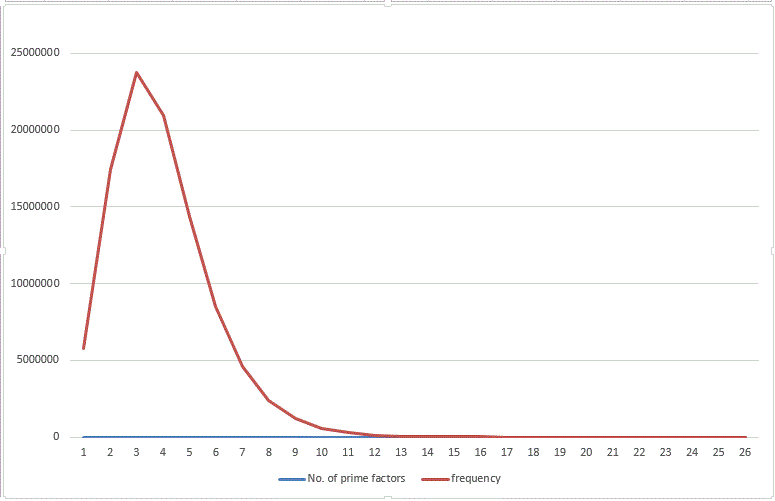
Graph of Prime factor distribution from $0$ to $10^8$ :

Note :

If you have another idea (rather than line graph) of representing the data then please share!
Thanks to Páll Márton to submit answer till $10^8$ .

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

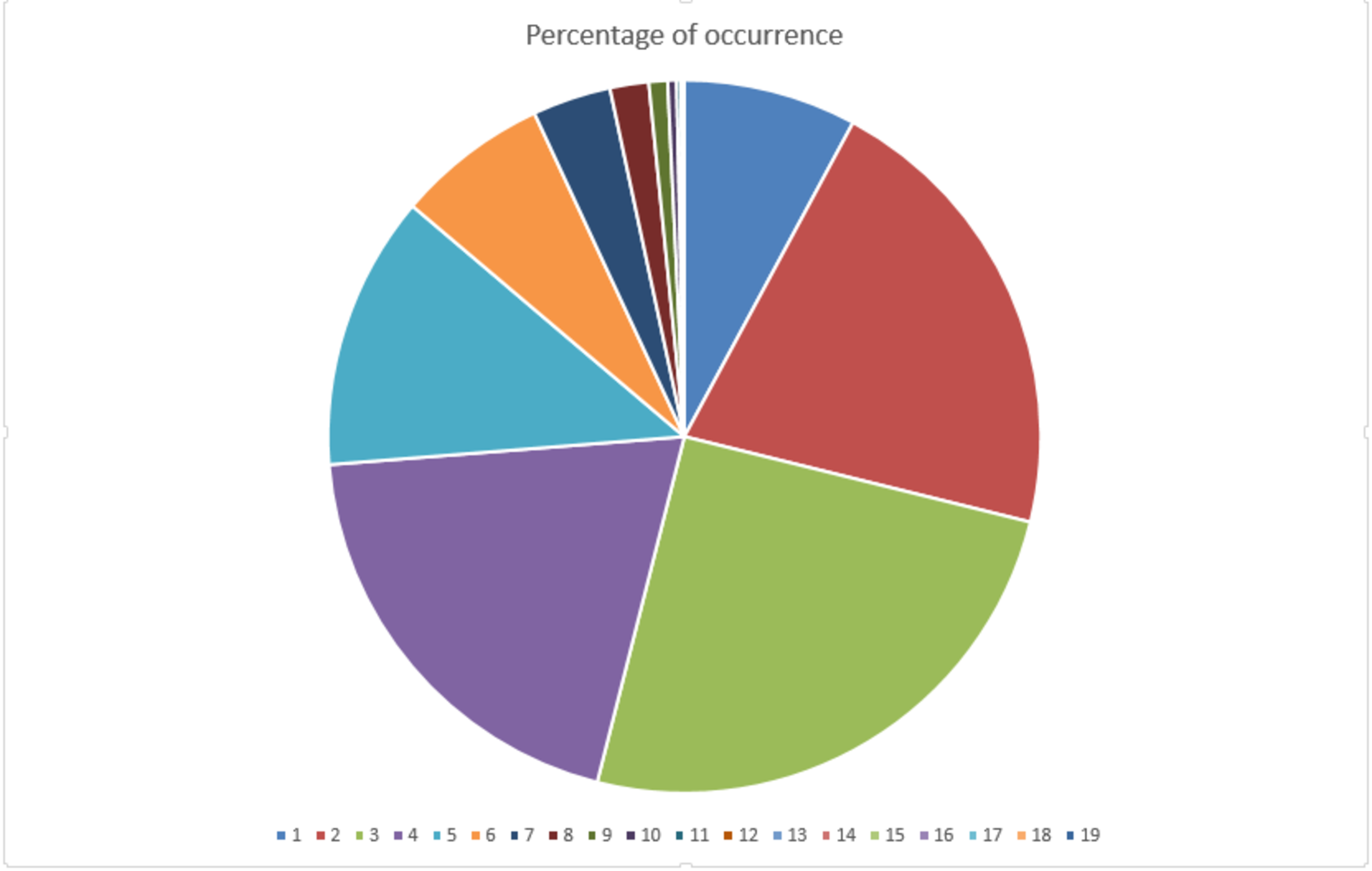
@Zakir Husain I think Pie chart will be better as it will help visualise more clearly.

Aryan Sanghi - 10 months, 3 weeks ago

Sure!

Zakir Husain - 10 months, 3 weeks ago

It seems that till $10^6$ numbers with number of prime factors - $2,3,4$ are most common. Also highly composite number are more rare than primes

Zakir Husain - 10 months, 3 weeks ago

Reminds me of $\dfrac{1}{(x-k)^n}$ ...

Jeff Giff - 10 months, 3 weeks ago

What? I didn't understood, what you meant?

Zakir Husain - 10 months, 3 weeks ago

x=number of prime factors, k & n are unknown constants, the output of the function is the number of number that have x prime factors.

Jeff Giff - 10 months, 3 weeks ago

Matches the graph

Jeff Giff - 10 months, 3 weeks ago

@Jeff Giff – Are you asking or telling???

Zakir Husain - 10 months, 3 weeks ago

@Jeff Giff – Except for $x < 2$ I guess?

David Stiff - 10 months, 3 weeks ago

Looking great @Zakir Husain ! Could you share the actual numbers as well?

David Stiff - 10 months, 3 weeks ago

$\Large{Announcement:}$ New plan is here, everything is nearly changed now

Zakir Husain - 2 months, 3 weeks ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$