Analytic solution for areas ratio

Find the ratio of the red area to the blue area. Regular heptagons are equal.

Inspiration1

Inspiration2 -Septic Triangle

Phyton give 2.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
from math import isclose
from sympy import *

radius = csc(pi / 7) / 2  # arrange for side length = 1
center = Point(0, 0)  # centered at Origin
p = Polygon(center, radius, n=7)
side = trigsimp(p.sides[0].length)
assert (isclose(side, 1, abs_tol=1e-30))

A, B, C, D, E, F, G = p.vertices
print(A)
print(B)
AE = Line(A, E)
GC = Line(G, C)
BF = Line(B, F)
GB = Line(G, B)
FA = Line(F, A)
P = FA.intersection(GB)[0]
H = AE.intersection(GC)[0]
J = AE.intersection(BF)[0]
I = GC.intersection(BF)[0]
area = Triangle(H, I, J).area*7
Big_area = Triangle(Point(0,0),A,B).area*7
Lit_area = Triangle(Point(0,0),J,I).area*7
SideL_area = Triangle(G,A,P).area*7
SideB_area = Triangle(G,A,H).area*7
S= Big_area-SideL_area-Lit_area-area
s= Big_area-SideB_area-Lit_area
print(S/s)
S_area = N(S, 20)
s_area =N(s,20)

print(S_area)
print(s_area)
print(S_area/s_area)


(-7*(-9 + cos(pi/14)/sin(pi/7) + 4*cos(3*pi/14)/sin(pi/7))/(32*(sin(pi/14) + 1)*sin(pi/14)*sin(pi/7)) - 7*(1 - sin(3*pi/14))*(-cos(3*pi/14) + cos(pi/14))/(4*(-sin(pi/7) + sin(2*pi/7) + cos(pi/14))*sin(pi/7)) - 7*(-cos(3*pi/14) + cos(pi/14))*(-789*cos(2*pi/7)/(8*sin(pi/7)) - 789*sin(3*pi/14)/(8*sin(pi/7)) - 385*sin(pi/14)/(4*sin(pi/7)) - 15*sin(5*pi/14)/(4*sin(pi/7)) - 15*(1 - cos(2*pi/7))**2*cos(2*pi/7)/sin(pi/7) - 23*(1 - cos(2*pi/7))**2*sin(pi/14)/sin(pi/7) - 3*(1 - cos(2*pi/7))**2*sin(3*pi/14)/sin(pi/7) + 9*(1 - cos(pi/7))**2/(2*sin(pi/7)) + 43*cos(3*pi/7)/(8*sin(pi/7)) + 2*(1 - cos(3*pi/7))**2/sin(pi/7) + 35*(1 - cos(2*pi/7))**2/(4*sin(pi/7)) + 10*(1 - cos(2*pi/7))**2/tan(pi/7) + 36/tan(pi/7) + 901/(8*sin(pi/7)))/(32*(sin(2*pi/7) + 2*sin(pi/7))*(-sin(pi/7) + sin(2*pi/7) + cos(pi/14))*(-6*cos(pi/14) + 5*sin(pi/7) + 4*cos(3*pi/14))*sin(pi/14)*sin(pi/7)**2) + 7*sin(2*pi/7)*csc(pi/7)**2/8)/(-7*(-48*sin(pi/7) - 22*cos(5*pi/14) - 7*sin(2*pi/7) + 35*cos(pi/14))/(4*(-60*cos(2*pi/7) - 49*sin(3*pi/14) - 75*sin(pi/14) - 20*sin(2*pi/7)**2 - 6*cos(pi/7) - 8*cos(2*pi/7)*cos(3*pi/7) + 8*cos(3*pi/7) + 38*sin(5*pi/14) + 66)) - 7*(1 - sin(3*pi/14))*(-cos(3*pi/14) + cos(pi/14))/(4*(-sin(pi/7) + sin(2*pi/7) + cos(pi/14))*sin(pi/7)) + 7*sin(2*pi/7)*csc(pi/7)**2/8)

2.4356342034533018176

1.2178171017266509088

2.0000000000000000000

#Geometry

Note by Yuriy Kazakov
3 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

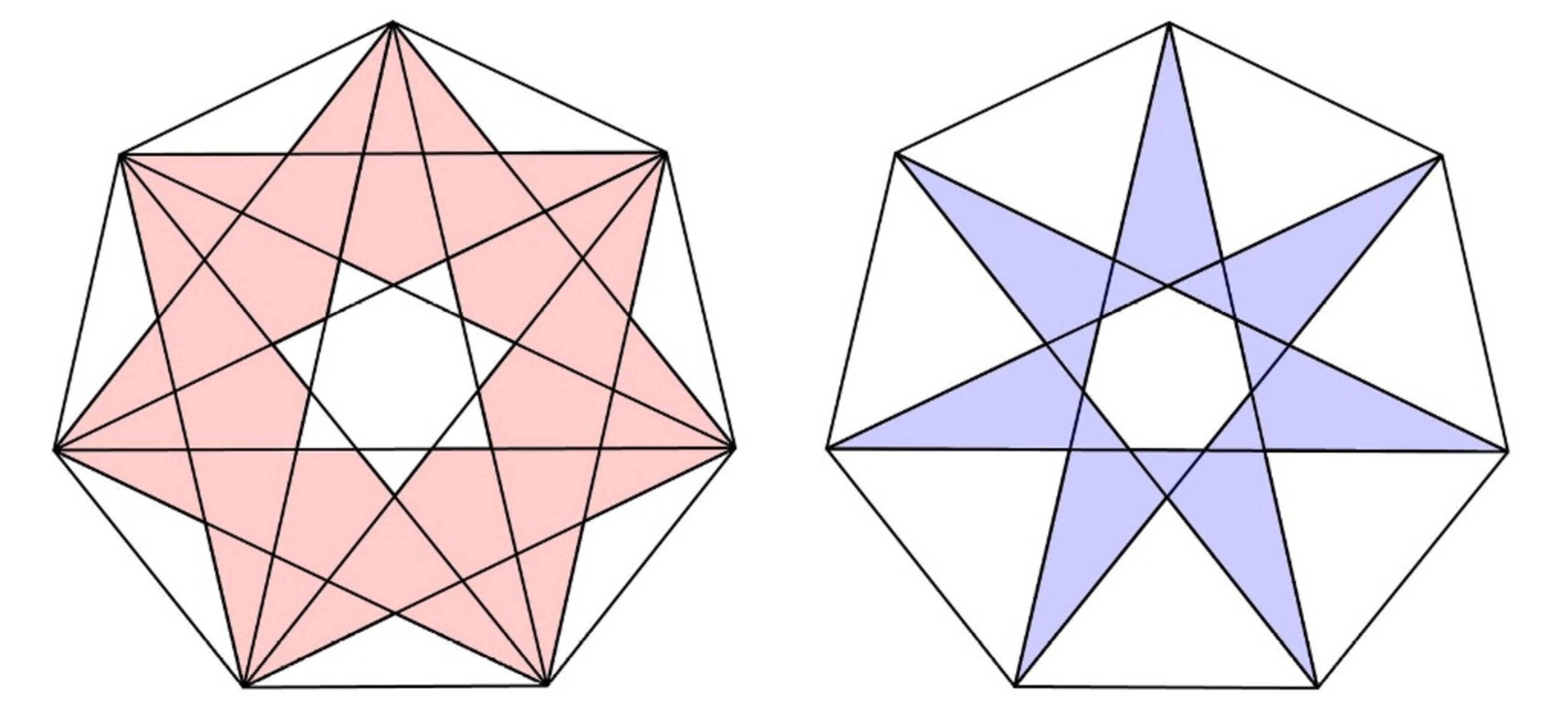
As simple as that - we cut the big star into 21 pieces and make up two identical stars - one of the red and the second of the yellow and blue pieces.

Yuriy Kazakov - 3 months ago

Log in to reply

That's...incredible. Simply amazing Yuriy!

David Stiff - 3 months ago

Sympy! Cool!

David Stiff - 3 months ago

Yeah, sympy is fun to play with, isn't it? I wish it were a little better at simplifying trig expressions, though. That one is frightening me. :)

Fletcher Mattox - 3 months ago

Problem - find solution without Sympy. Only paper and pencil.

Yuriy Kazakov - 3 months ago

You should tweet this to Cshearer41 on Twitter with a caption of

"Prove that the area of the pink region is twice the area of the blue region"

Pi Han Goh - 3 months ago
×

Problem Loading...

Note Loading...

Set Loading...