Another construction problem. A pretty easy one this time.

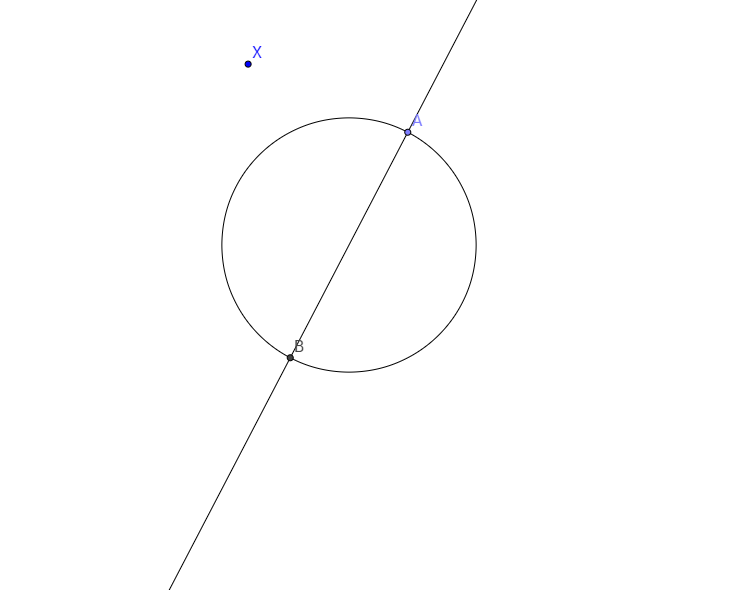Using a straightedge, (a ruler with no markings that you can use to join two points) find a way to draw a perpendicular through a given point X that is arbitrarily placed on a plane that contains a circle with a given diameter AB.

Also, state the conditions for point X so that your procedure is valid.

I am very pleased to say that I figured it out in the exam hall pretty quickly. And this is from today's / this year's CMI entrance exam paper.

Okay, here's how you do it:

Join X and A and X and B. Let XA meet the circle at Y and XB meet the circle at Z.

Now, join B and Y and A and Z. The meeting point of BY and AZ will be the orthocentre (W) of triangle XAB.

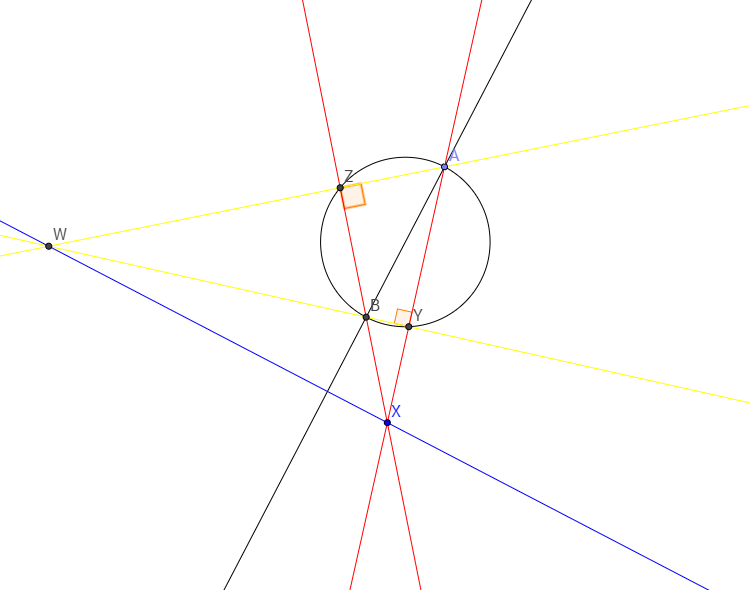
Join XW. Now, XW is perpendicular to AB.

QED.

But is this possible for any point X?

No.

There are three regions in the given plane:

  • inside of the circle
  • outside of the circle
  • circle.

If X lies in the first two regions, then there's no problem. But if X lies on the circle, then X would be the orthocentre as XAB would be a right angled triangle and X=W. So, you can't join X and W because they're the same point. And there are infinitely many lines that can be drawn through a point.

#Geometry

Note by Vishnu C
6 years ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

@Michael Mendrin I thought you'll enjoy solving this one as well. Try not to make a messy figure this time : )

vishnu c - 6 years ago

Ramesh Goenka - 6 years ago

Log in to reply

What exactly do you mean by the crossed out/ "wrong" lines?

vishnu c - 6 years ago

Log in to reply

In the crossed out, or "wrong" lines that you've posted, the triangle XAB is an obtuse angled triangle. So if you produce XB to meet the circle at Z, then AZ would be perpendicular to XZ and if the point of intersection of XA and the circle is Y, then the meeting point of BY and AZ would give the orthocentre (W) again. So why is it wrong?

vishnu c - 6 years ago

Log in to reply

@Vishnu C – dint considered that .. !! u r right :D

Ramesh Goenka - 6 years ago
×

Problem Loading...

Note Loading...

Set Loading...