Anyone help !!!
I found this problem was very difficult :(. Can anyone help me solve this? Here is the problem:
Given a parabola . Find the ratio of two inscribed circle on the parabola, both bordered by the parabola and the axis. But one circle is over axis and the other one is under axis.
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
the length of the circumference O1 = 15.71(approximately)
the length of the circumference O2 = 9.43(approximately)
Co1/Co2 = 1.7
Calculations made with Geogebra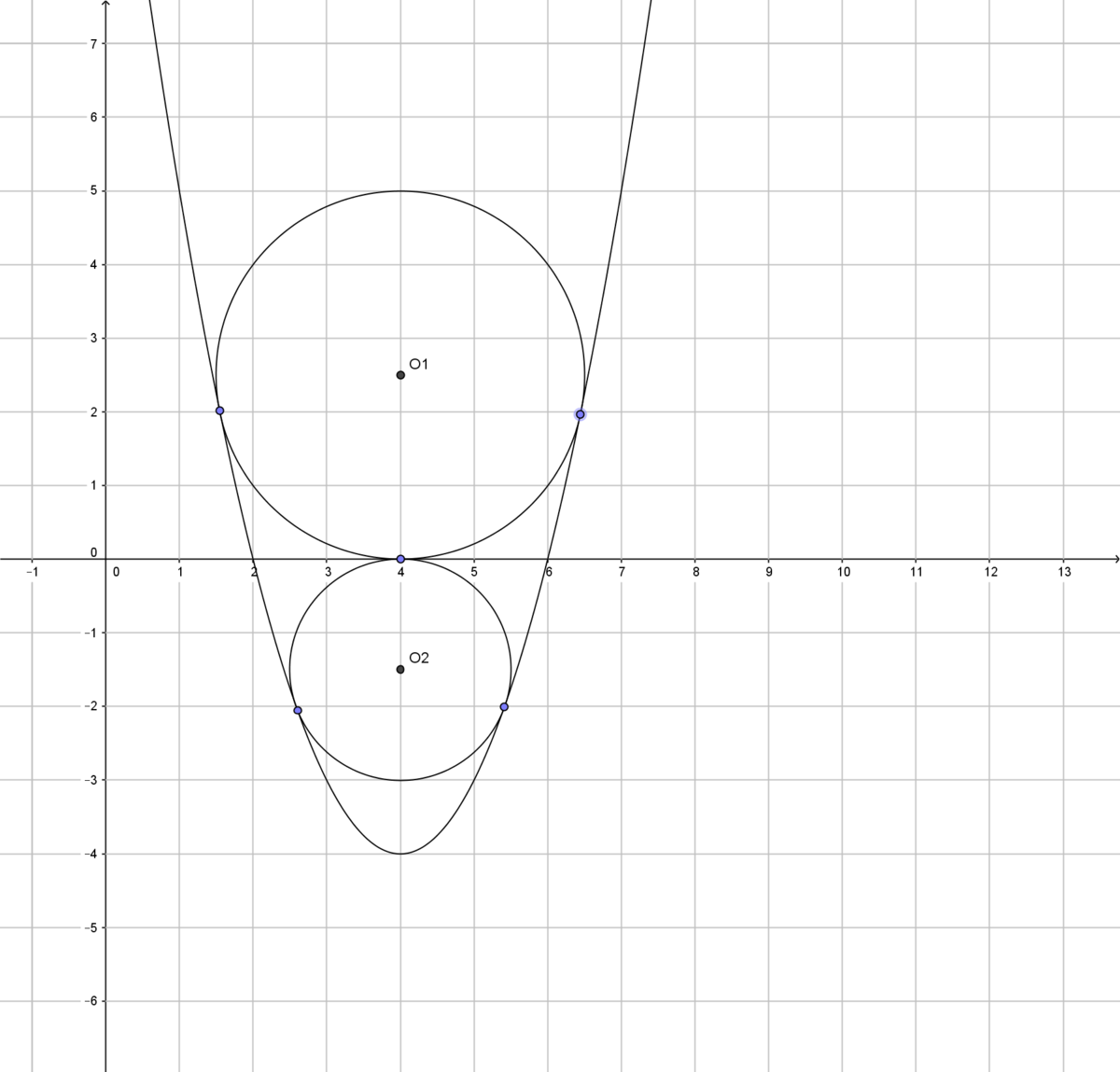
Log in to reply
Is there no other 'common' way to solve this problem? I mean without using software? I just want to know how to solve this problem. But firstly, thank you so much for your help.
Log in to reply
I don't know English very well, but I'll try to help you :
First of all let's rewrite our function in this form (it will be the same result at the end since I am using Translation (geometry)):
f(x)=x2−4
Then we must find the coordinates of the vertex of our new parabola and roots of x2−4=0
Here it is :
1) coordinates of the vertex : x=0 and y=−4 ,so : (0;−4)
2) roots : x=±2 , also we have two points : (−2;0) and (2;0)
So, now we should define some points (take a look at my picture) : A(0;−4) , B(−2;0) , C(2;0) also let's suppose that O1 and O2 are the centres of our circles, where O1(red)(0;y) and O2(0;y1) .
Let's take a look at triangle ABC :
AB=AC=20(by Pythagorean theorem) and SΔABC=8
Let's draw circumcircle O3(orange) of the triangle ABC and find it's radius : R=4SABCAB∗BC∗CA, where R=2.5 .
So, the centre of O3 is obviously point (0;−1.5)
/**********************************************************
Let's suppose that point (0;−1.5) is also the centre of circle O1. It means, that R(O1)=1.5.
To prove that point (0;−1.5) is the centre of O1 we must prove that line segment LO1=1.5.
Straight line LO1 is a normal- line that is perpendicular to our parabola in point L.
So, here it's function : f(x)=−2x01(x−x0)+(x02−4) (x0 is the touch abscissa(point L) of the parabola and circle O1)
Let's find x0. Under our assumption point O1 has the following coordinates (0;−1.5). Now we must put them in our normal function.
−2x01(0−x0)+(x02−4)=−1.5
Where x0=−1.414213562. Now we must put x0 in the parabola function.
y=(−1.414213562)2−4 , y=−2. Ordinate of point L=−2. So, L=(−1.414213562;−2)
Now, we should check if ∣LO1∣=∣O1D∣=1.5
∣LO1∣=(0−(−1.414213562))2+(−1.5−(−2))2=1.5.
Our assumptions were confirmed =) . So point (0;−1.5) is the centre of circle O1. And of course ∣O1D∣=RO1=1.5
/**********************************************************
Now, the next part of my horrible solution.
It's much easier to find the centre of O2.
Let's assume that the straight line KB coincides with our parabola (y∈(0;6)) and tangent line to the parabola at point B(−2;0)
So, we can find tan(∠KBD)
Firstly, let's find the tangent line function : it's f(x)′=(x2−4)′=2x then put abscissa of point B in this function.
So, f′(−2)=−4=tan∠KBD⇒∠KBD≈104∘
Since KB and BD are tangents to the circle O2 ⇒ KB=BD. Also KO2=O2D ⇒ O2B-bisector and median ⇒ O2BD≈52∘
tan∠O2BD≈1.28 ⇒ 1.28=DBO2D=2O2D ⇒ O2D=2.5
O2=(0;2.5) ⇒ RO2=2.5
/**********************************************************
And of course the last step :
RO2RO1=0.6
That's it =)
Log in to reply
Thank you very much Fatum. My english is not very good also :)
Log in to reply
But why exactly this problem, why did you want to solve it?
Log in to reply
I just randomly solve problem from my book. And from those problems, I just can't solve this one
Log in to reply
What book?
Log in to reply
Text book. I'm a student of high school
Both the circles touch X axis at (4,0) by symmetry.We can interpret this as follows -these two circles are the members of family of circles that pass through through the intersection of line y=0 and the circle with centre (4,0) and radius 0.We know that S+ku=0 represents family of circles passing through intersection of circle S=0 and line u=0 where k is arbitrary parameter.Now solve the equation of circle and parabola to obtain a quadratic equation in y.Since the parabola and circle touch each other set the discriminant of the quadratic as 0.This will give two values of k namely 3 and -5.The two values of k give us the two equations of the circles.