Area Between Two Tangents on a Circle Equation

$a_{t}=\dfrac{r^{2}}{\tan\left ( \dfrac{\beta}{2} \right )}- \dfrac{\pi \cdot r^{2}\alpha}{360}$

Here is an equation I derived in a simple manner for finding the area between two tangents on a circle in terms of the radius if given their angle of intersection, as shown above.

In accordance with this diagram:

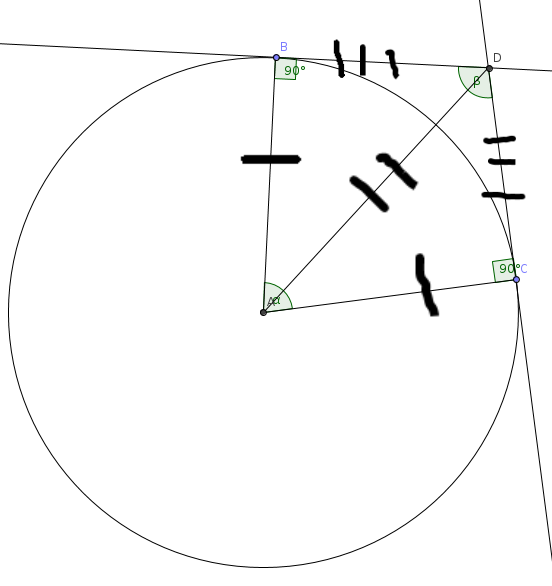
We can prove with SSS or SAS that the two triangles are congruent. Here, beta is the angle of intersection and beta is the supplement of alpha. All I am doing is finding the areas of both triangles and subtracting from it the area section of our circle, whatever remains is the area between the curves. Nothing fancy, but it is nice to generalize something, and it might come in handy for someone somewhere.

#Geometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

This formula would look a little neater if you'd have expressed all angles in radians.

A Former Brilliant Member - 5 years, 3 months ago

@Deeparaj Bhat Right. So I guess: $\frac {r^{2}}{tan (\frac{\beta}{2})}- \frac{r^{2}\alpha} {2}$ . You are right, it looks a lot nicer. I tried also getting a common denominator, but that looks even worse than using degrees. Thank you, sir.

Drex Beckman - 5 years, 3 months ago

@Drex Beckman On plugging in $\beta$ , the formula becomes,

$\frac{r^2}{2}\cdot(\tan{\frac{\alpha}{2}}-\frac{\alpha}{2})$

A Former Brilliant Member - 5 years, 3 months ago

@A Former Brilliant Member – @Deeparaj Bhat Can you please tell me how you derived that? Sorry, I'm lacking in maths. Is there an identity you used? Also, am I doing something wrong? I tried this with my question: $\frac{r^{2}}{2}(tan (\frac {\alpha}{2})-\frac{\alpha}{2})$ where $\alpha = 0.479965 radians$ , and I got an answer of $\approx 0.00236$ , which is exactly half the answer. I think it should be r squared itself, not divided by two, right? I tried this with different r, too. Thanks for your help, it is really appreciated!

Drex Beckman - 5 years, 3 months ago

@Drex Beckman – Sorry, my bad. It was supposed to be $r^2(\tan{(\frac{\alpha}{2})}-\frac{\alpha}{2})$ , like you said.

I used the following two facts for deriving it:

$\alpha+\beta=\pi$ $\tan{(\frac{\pi}{2}-x)}=\cot{x}$

The first follows by the fact that sum of angles in a quadrilateral ( here ABCD) is $2\pi$ and since $\angle ACD=\angle ABD=\frac{\pi}{2}$

The second is a well known identity which you can find in one of wikis on Brilliant.

A Former Brilliant Member - 5 years, 3 months ago

@A Former Brilliant Member – Okay, I get it now. I don't really remember lots of trig identities, so I should obviously review them. :P But you did a great job simplifying it. It really does look a lot more beautiful that way. Thanks! :D

Drex Beckman - 5 years, 3 months ago

@Drex Beckman – In fact, most of the level 5 geometry problems can be solved (almost) exclusively by using trig identities!

A Former Brilliant Member - 5 years, 3 months ago

@A Former Brilliant Member – Seriously?! Good to know, man. I learned them at school a few years ago, and never used them again. But that was before I thought mathematics was fun. Too bad I didn't get interested in it earlier, because I am way far behind people like you, also I think most of the people on here are smarter than me. xD

Drex Beckman - 5 years, 3 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$