Area Created by Joining Every Kth Vertex in a Polygon

\(~\)\(~\)\(~\)\(~\)\(~\)\(~\)\(~\)\(~\)\(~\)In this note, I will prove that the area formed by connecting every kth vertex of a regular polygon is \(\dfrac{a^2n(\cot{\frac{180k_i}{n}})(\csc^2{(\frac{180}{n})})(1-\cos{(\frac{k_i360}{n})})}{8k_i}\) when \(\textbf{k divides n without remainder}\) and n=number of sides of the original polygon and a represents the side length of the original polygon.

$~$$~$$~$$~$$~$$~$$~$$~$$~$ Can someone link me to a website so I can read up on it? I haven't been able to find one.

Step one: determining the number of sides

$~$$~$$~$$~$$~$$~$$~$$~$$~$This step is rather simple. The number of sides of the original polygon R divided by k will yield the new polygon’s number of sides.

$~$$~$$~$$~$$~$$~$$~$$~$$~$This is because #vertices=#edges. And since we’re dividing the number of vertices by k, the number of edges will be divided by k as well.

$~$$~$$~$$~$$~$$~$$~$$~$$~$Therefore, the number of sides $=\boxed{\dfrac{n}{k_i}}$

Step two: determining the length of each side

image

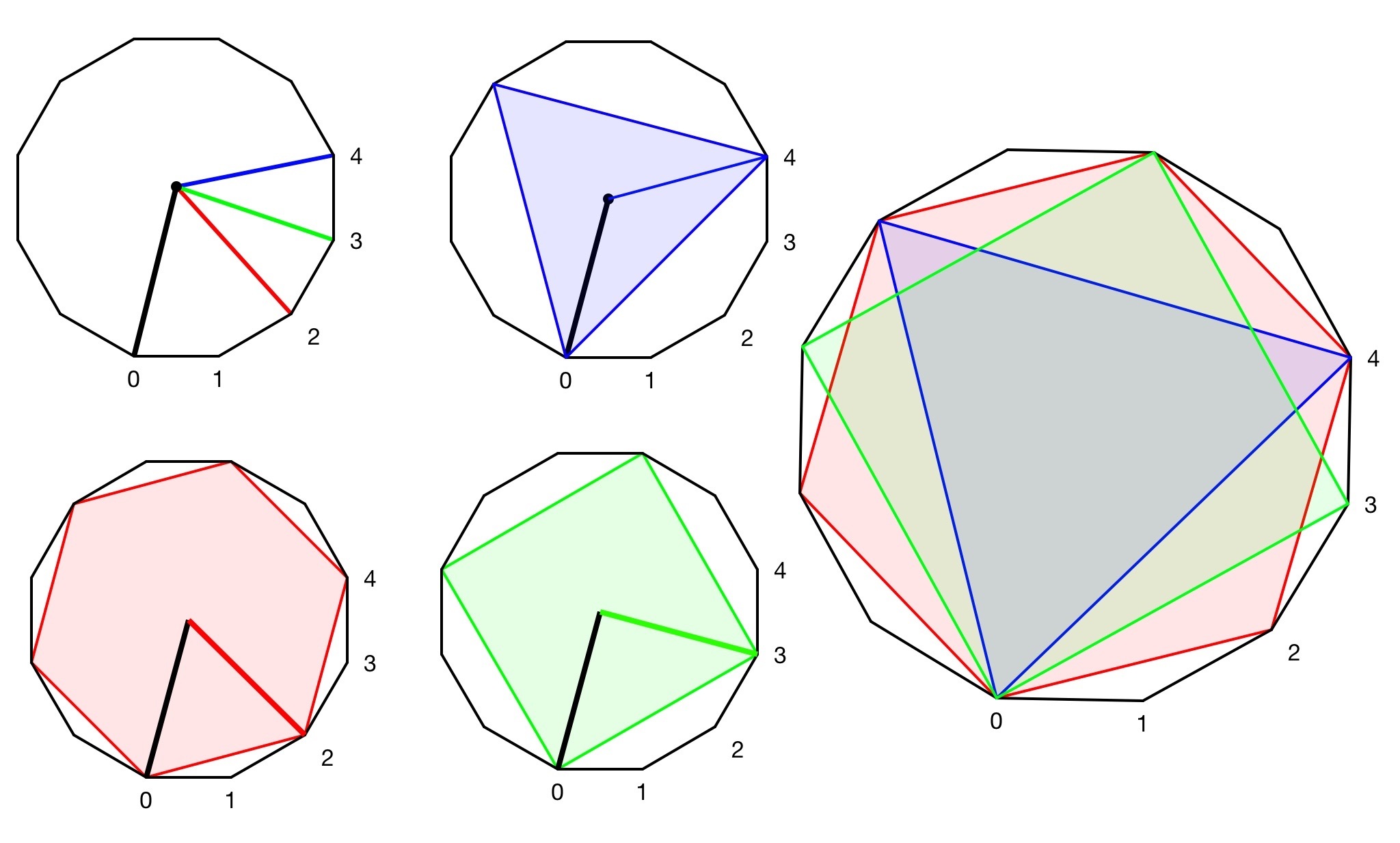
$~$$~$$~$$~$$~$$~$$~$$~$$~$Ok, this is the hard part. For this part, I will refer to the second picture (also, NOTE 1,2,3,4 represent possible values of k). Begin by looking at the angled formed by $\theta$. It’s quite obvious that each angle is congruent. Also, $\boxed{\theta=\frac{360}{n}}$. Now, if we’re going to connect every kth vertex starting with vertex J, the angle (NOTE: point k varies in position) formed will be equal to $\boxed{\angle{JPK_i=k_i\theta}}$.

$~$$~$$~$$~$$~$$~$$~$$~$$~$Now, the one thing that remains constant no matter what vertex we chose is the length from the center of the original polygon to each vertex, AKA: the radius. The radius r is the hypotenuse of a right triangle with one leg as its apothem and the other leg being $\frac{a}{2}$. The angle at P of the right triangle is $\dfrac{\theta}{2}$. Therefore, $\boxed{r=(\frac{a}{2})\csc{(\frac{\theta}{2})}}$.

$~$$~$$~$$~$$~$$~$$~$$~$$~$Now, using Law of Co-sines, we can find M (length of segment $\overline{Jk_i}$) in terms of $k_i\theta$ and r (r is in terms of a and $\csc$ here).

$m^2=r^2+r^2-2(r)(r)\cos{(k_i\theta)}$

$m^2=2r^2(1-\cos{(k_i\theta}))$

Substituting for $r=(\frac{a}{2})\csc{(\frac{\theta}{2})}$

$m^2=2\left[(\frac{a}{2})\csc{(\frac{\theta}{2})}\right](1-\cos{(k_i\theta)})$

Substituting for $\theta=\frac{360}{n}$

$m^2=2\left[\frac{a^2\csc^2{(\frac{(\frac{360}{n})}{2})}}{4}\right](1-\cos{(k_i(\frac{360}{n})})$

$\boxed{m^2=\dfrac{a^2\csc^2{(\frac{180}{n})}(1-\cos{(\frac{360k}{n})})}{2}}$

Finding the area

$~$$~$$~$$~$$~$$~$$~$$~$$~$This step isn't so hard, in this note, I prove that the area of any regular polygon can be represented as $\dfrac{ \left(\dfrac{n}{k_i}\right)\cot(\dfrac{180k_i}{n})m^2}{4}$. (NOTE: that I substituted a=m from the other note and the number of sides is $\dfrac{n}{k_i}$ rather than n because in this note I’m using different variables than in the other note)

Plugging in our value of $m^2$ yeilds

$area=\dfrac{\left(\dfrac{n}{k_i}\right)\cot{(\dfrac{180k_i}{n})}\left(\dfrac{a^2\csc^2{(\frac{180}{n})}(1-\cos{(\frac{360k_i}{n})})}{2}\right)}{4}$.

$area=\dfrac{ n\cot{(\dfrac{180k_i}{n})}\left(a^2\csc^2{(\frac{180}{n})}(1-\cos{(\frac{360k_i}{n})})\right)}{8k_i}$.

$\boxed{area=\dfrac{a^2n(\cot{\frac{180k_i}{n}})(\csc^2{(\frac{180}{n})})(1-\cos{(\frac{k_i360}{n})})}{8k_i}}$