Area of a Circle Part 2

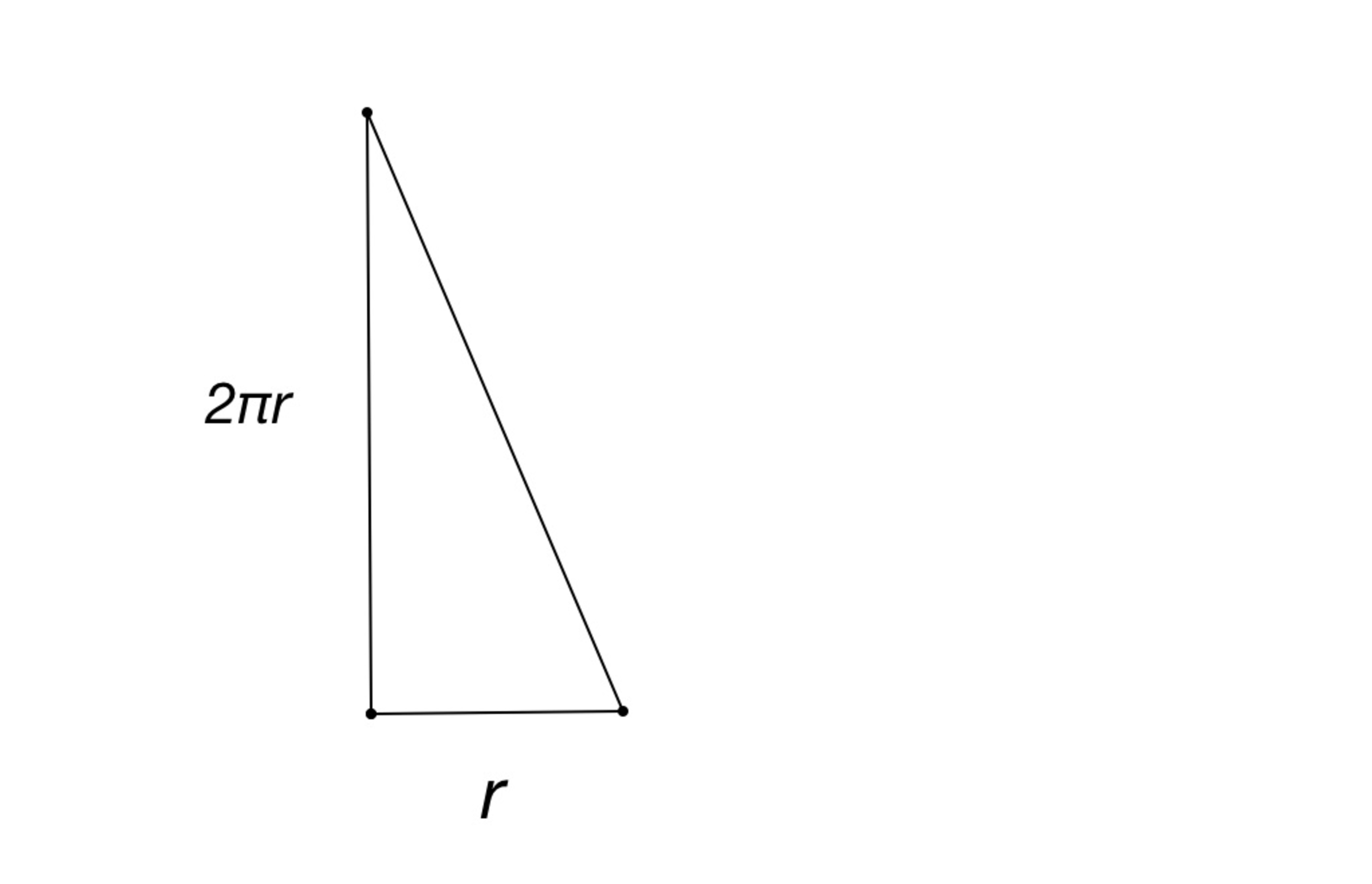
In the first part, we divided a circle into infinitely many rings to attempt to find the area. We now have many lines of increasingly smaller length. But how can we answer the question of turning these lengths into an area?

Let's begin by thinking about these rings laid out as lines. The first line is the circumference, with length 2πr2 \pi r. If they are all laid out with one end at equal height as the others, then the other end of each line will be shorter by a certain amount compared to the previous one. Since the "radius" of each of these rings is shorter than the last, the circumference of each ring, or it's length, is shorter, all the way down to the point in the center of the circle. This gradual decrease in line height starts to look line a line itself. Now, with enough lines or rings laid out in this way, the whole thing starts to resemble a shape.

A triangle, to be exact. The triangle's height is the circumference 2πr2 \pi r , and the base is the radius rr, as we took rings from the farthest reach of the radius to the center.

Now, we simply use the formula for a triangle's area, A=12bhA = \frac{1}{2} bh. Substituting in our values we get:

A=12⋅2πr⋅rA = \frac{1}{2} \cdot 2 \pi r \cdot r

=12⋅2πr2= \frac{1}{2} \cdot 2 \pi r ^ 2

=πr2= \pi r ^ 2

#Triangle #Infinity #Circle #Radius

Note by Stephen Shamaiengar
7 years, 3 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

This is awesome! Never thought of it like this... but you have to be careful. When dealing with axiomatic properties and postulates, you can't prove a postulate with that postulate. For example, I shouldn't try to use the Pythagorean theorem to prove the Pythagorean theorem :P. The reason I am addressing this in this case is because if you look at the proof that the area formula is correct, it is based on the circumference formula. But still, great job!

Finn Hulse - 7 years, 3 months ago

Log in to reply

Yea I understand. Thanks

Stephen Shamaiengar - 7 years, 3 months ago
×

Problem Loading...

Note Loading...

Set Loading...