Area of a Circle

Have you ever wondered where the formula A=πr2A = \pi r ^ 2 comes from?

The explanation is quite simple, and is based somewhat on Calculus concepts like limits.

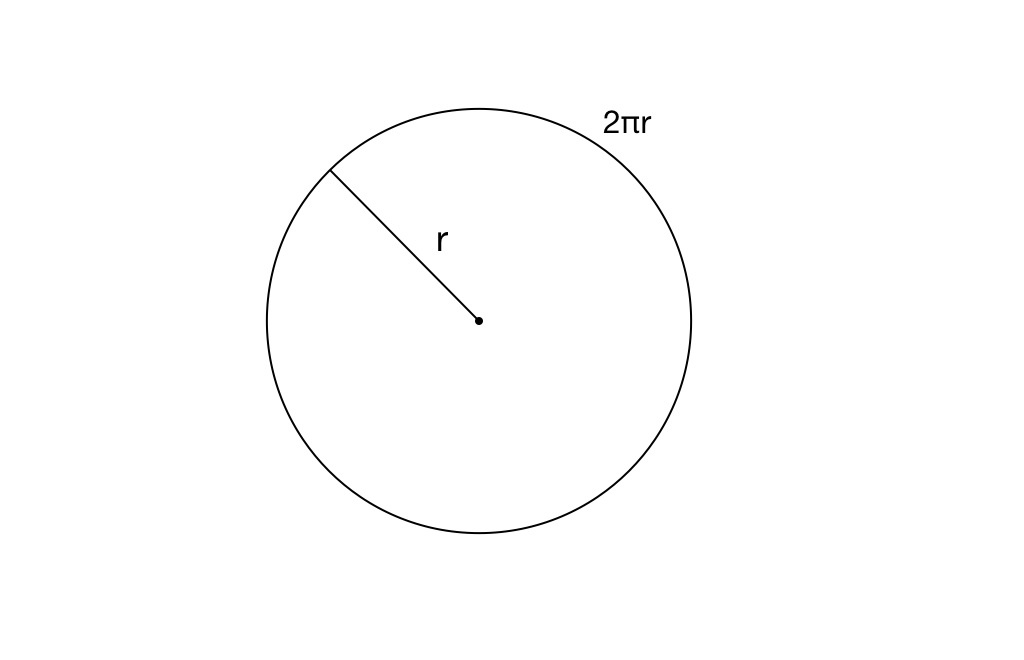
Take a circle, like the one above. The radius is rr and circumference 2πr2\pi r . How could one figure out the total space inside it easily, without trying to fit tons of nn-gons in it like Archimedes? We can't use squares or polygons because they are not totally accurate. They leave out space on the edge. But who said we have to work with shapes? Let's work with lines; more specifically, curves, like the one we are given.

What if you divided the circle up into rings, infinite amounts of them, so that they covered the entire circle? Starting with the circumference as the first ring and working inwards, the rings get constantly and gradually shorter. Thinking of each ring as the circumference of a smaller and smaller circle, the radius is getting smaller proportionally to the circumference. Eventually, we get to a point in the middle, a ring with 0 length. Now that we have this infinite amount of lines, you may ask, what can we do with these? How can we turn 1-dimensional lengths into a 2-dimensional area?

The answer in part 2.

#Area #Infinity #Circle

Note by Stephen Shamaiengar
7 years, 3 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Cool beans! You can put other pictures into your notes though.

Conor Sokolowsky - 7 years, 3 months ago

Log in to reply

Thanks, it's okay though I just made it separate.

Stephen Shamaiengar - 7 years, 3 months ago
×

Problem Loading...

Note Loading...

Set Loading...