Area of Circle - It's different!!

This is a series that was made by me some days before.

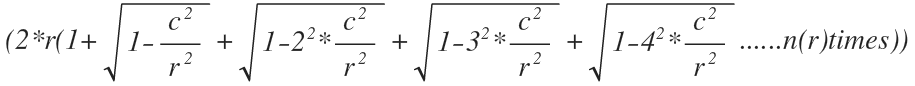
This series gives us the area of a semi-circle. In the above series: 'r' represents the radius of the circle, n(r) is the numeric value of the radius, n(r) gives us the number of terms that we have to take inside the brackets, 'c' is a variable that has different values for different radii.

The inequality for 'c'

For radii = 2 and 3,

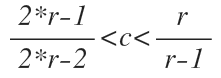
For other values of radius,

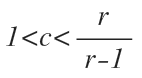
If we chose an appropriate value of 'c' as per the inequality, the series will give us a roughly accurate answer. If luckily we chose the right value of 'c' then the equation will give us an accurate answer.

For example, for radius = 2, the value of 'c' = 1.641 will give us an accurate answer.

Let us solve for the area of circle of radii = 2 cm .

Taking c =1.641 (as per the inequality)

Therefore, as per the series, we only take 2 terms inside the brackets as the numeric value of radius is 2.

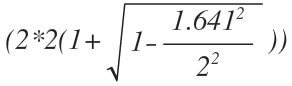
further simplifying gives us the following result,

If we calculate the area of semicircle using, 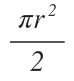we get the area of semi-circle=6.28.

I hope you all liked this and I keenly look forward for your inputs and comments.

#Geometry

Note by Nippun Sharma
4 years, 5 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

good work brillant

Lavanya Sharma - 1 year, 1 month ago
×

Problem Loading...

Note Loading...

Set Loading...