Area of Square Inside Two Concentric Squares

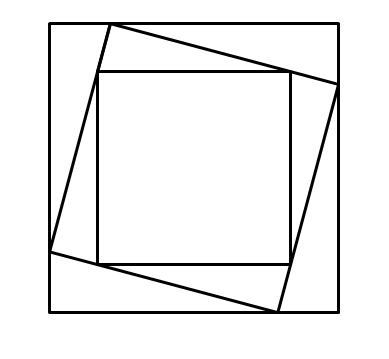
Let two squares of side lengths \(a\) and \(b\) with \(b<a\) be positioned so that their centers coincide and that corresponding sides are parallel, as shown. Draw a square \(\mathcal{S}\) so that it is inscribed inside the square of side length \(a\) but circumscribes the square of side length \(b\).

  1. What restrictions must be placed on aa and bb so that such a square exists?

  2. Show that under the conditions laid out in the previous part, square S\mathcal{S} has side length equal to ab\sqrt{ab}.

NOTE: This discovery was first found by a friend of mine in response to a problem I had created.

#Geometry #Square #Proofs

Note by David Altizio
7 years ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

2b>a

Сергей Кротов - 7 years ago

Let θ \theta be the smaller angle that the diagonal makes with one of the sides. Let d d be the side of the middle square. Then a=d(sin⁡θ+cos⁡θ) a = d (\sin \theta + \cos \theta) and d=b(sin⁡θ+cos⁡θ) d = b (\sin \theta + \cos \theta) . So a=b(sin⁡θ+cos⁡θ)2 a = b(\sin \theta + \cos \theta)^2 . It's easy to see that 1≤sin⁡θ+cos⁡θ≤2, 1 \le \sin \theta + \cos \theta \le \sqrt{2}, so the condition boils down to a≤2b a \le 2b .

The area of the square is d2=b2(sin⁡θ+cos⁡θ)2=ab d^2 = b^2 (\sin \theta + \cos \theta)^2 = ab , so the side is ab \sqrt{ab} .

Patrick Corn - 7 years ago
×

Problem Loading...

Note Loading...

Set Loading...