Atmospheric physics 4: Ideal gas

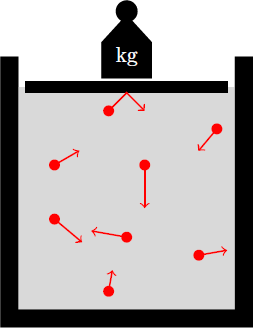
Dry air behaves in good approximation as an ideal gas and therefore follows the general gas equation: \[ \boxed{P = R \dfrac{n}{V} T = R^\ast \rho T} \] where

• $P$ is the pressure
• $n$ is the amount of substance (in units of mols)
• $V$ is the volume
• $\rho = M n/V$ is the mass density with the molar mass $M$
• $T$ is the absolute temperature (in units of Kelvin)
• $R \approx 8.314 \,\text{J}/\text{mol}\,\text{K}$ is general gas constant
• $R^\ast = R/M$ is the specific gas constant

Ideal gases have a low particle density, so there is virtually no interaction between the molecules (except for rare collisions). Thus, the gas particles have random positions and velocities, that are completely uncorrelated. Therefore, the thermodynamic properties of the ideal gas can be derived from the kinetic theory of gases. Here we briefly outline the arguments that can be used to derive the general gas equation. The temperature $T \propto \langle E_\text{kin} \rangle$ of the gas is a measure of the kinetic energy of the individual particles. The pressure on the walls of the container arises because the molecules regularly hit the walls, each transmitting an impulse per second, which is proportional to its kinetic energy. The pressure generated by this collisions is thus proportional to the temperature and the (mass) density of the gas. Thus, the general gas equation results except for a constant pre-factor:

$\text{pressure } P = (\text{constant}) \cdot (\text{density } \rho) \cdot (\text{temperature } T)$