Ball Thrown Up An Inclined Plane

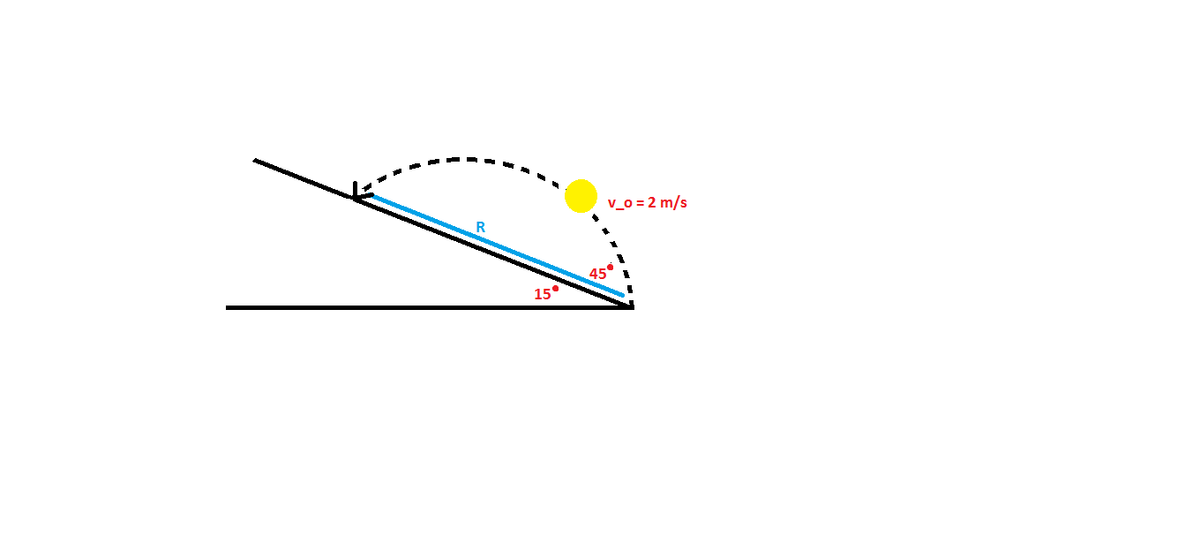
A yellow ball is thrown with initial speed $v_{0} = 2$ $m/s$ up an inclined plane. The plane is inclined at an angle $15 ^ \circ$ above the horizontal, and the ball's thrown with an angle $45 ^ \circ$ above the plane. If $R$ denotes the ball land's distance, find the value of $R$ . (assume $g = 10$ $m/s^2$ )

I found that the answer is $\frac{2}{5}(\sqrt{3} - 1)$ $m$ , but I'm not sure. Could anyone clarify? Thanks :)

#Physics #Mechanics #PhysicsProblem

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

$v_{x} = 2 \cos 60^\circ = 1$

$v_{y} = 2 \sin 60^\circ = \sqrt{3}$

$x = v_{x}t = t$

$y = v_{y}t - \frac{1}{2}gt^2 = \sqrt{3}t - 5t^2$

Because $\tan 15^\circ = \frac{y}{x},$ then $x = t = y(2 + \sqrt{3})$

By substituting $t = y(2 + \sqrt{3})$ to $y = \sqrt{3}t - 5t^2,$

$y = \sqrt{3}(2 + \sqrt{3})y - 5(2 + \sqrt{3})^2y^2$

$y(5(7 + 4\sqrt{3})y - 2(1 + \sqrt{3})) = 0$

Since $y \neq 0,$

$y = \frac{2(1+\sqrt{3})}{5(7+4\sqrt{3})}$

Because $\sin 15^\circ = \frac{y}{R},$ then $R = \frac{y}{\sin 15^\circ}$

Hence, $R = \frac{4\sqrt{2}(2-\sqrt{3})}{5}$

Fariz Azmi Pratama - 7 years, 9 months ago

Firstly, good question Nabila and great effort on your answer.

Fariz nice approach to the question, I completely agree with your answer as I verified it using a different method; which was finding the intercepts of the trajectory of the projectile and the plane.

I found using simple physics formulae that the height is $0.15m$

I then used this to model a formula for the trajectory; $y=ax^{2}+bx$ where b is the initial gradient of the projectile $tan(\pi/3)$ ,

Using height of $0.15$ , $a$ was found to be $-5$

Hence, $y=\sqrt{3}x-5x^{2}$ is the trajectory in the Cartesian coordinate system

This is now intercepted with the plane which is linear; $y=bx$ , were b is $tan(\pi/12)$

Therefore the plane is represented as; $y=(2-\sqrt{3})x$

Furthermore, the coordinates of the intercepts of the trajectory and the plane are calculated to be:

$y=\frac{6}{5}(\sqrt{3}-2)$ and $x=\frac{2}{5}(\sqrt{3}-1)$

Finally, using Pythagoras's Theorem, $R=\sqrt{(\frac{2}{5}(\sqrt{3}-1))^{2}+(\frac{6}{5}(\sqrt{3}-2))^{2} }$

Hence, $R=\frac{4}{5}\sqrt{2}(2-\sqrt{3})$

Joel Jablonski - 7 years, 9 months ago

Nice one!

Nabila Nida Rafida - 7 years, 9 months ago

Mathematical approach, cool :)

Fariz Azmi Pratama - 7 years, 9 months ago

Thanks, it seems my answer yet completed

Nabila Nida Rafida - 7 years, 9 months ago

Nice solution, though just a slight mistake in the end. I believe, you can easily get the right answer if you try to deduce a point in the trajectory where $\frac {y} {x} = \tan 15^\circ$ using the above equations. This would give the required R most probably.

Lokesh Sharma - 7 years, 9 months ago

Would you like to fix it, Lokesh? I'm not sure about my answer.....

Fariz Azmi Pratama - 7 years, 9 months ago

@Fariz Azmi Pratama – Referring to your solution, equation (3) and equation (4) define the trajectory of ball. The ball lands at the point $(x, y)$ such that $\frac {y} {x} = tan 15^ \circ$ .

Solving these three equations, the point can be located and hence the distance where the ball lands. Diving equation (4) with equation (3), $\frac {y} {x} = \sqrt3 - 5t$ and using $\frac {y} {x} = tan 15^ \circ$ , finally $\sqrt3 - 5t = tan 15^ \circ \Rightarrow \sqrt3 - 5t = 2 - \sqrt(3)$ .

Solving this we have $x = t =\frac {2 \sqrt3 - 2}{5}$ . Using trigonometry we get $\frac{x} {R} = cos 15^ \circ$ and hence $R = \frac{ x }{ cos 15^ \circ} \Rightarrow R = \frac {4(2 \sqrt3 - 2)}{5(\sqrt6 + \sqrt2)}$ .

Finally, $R = \frac {4(2\sqrt2 - \sqrt 6)}{5}$ which is same as yours. Hahaha. I was wrong about your solution. Sorry about that one.

Lokesh Sharma - 7 years, 9 months ago

@Lokesh Sharma – Haha it's okay.

Fariz Azmi Pratama - 7 years, 9 months ago

$Range=\frac{ 2*\sin45 }{ 5 *\cos^215 }$

Cody Martin - 7 years, 9 months ago

it should be 4 (sqrt2)/5

Viji Raj - 7 years, 9 months ago

Yes Victor is right. You may even use trigonometry sin 15 = (sqrt3-1)/2

Viji Raj - 7 years, 9 months ago

Hey, I think what you found was incorrect in the sense that what you found wasn't what the question was asking for. I found that your answer was what I got for the horizontal distance, not the actually length between the ball land's distance. What I did was find the equation for both lines (the inclined plane and the trajectory) find the intersection which is where you got, and the last bit is apply the Pythagorean theorem to get that length.

Victor Phan - 7 years, 9 months ago

$\frac{ 4 }{ 5 }(2\sqrt{6}-3\sqrt{2})$ ??

Cody Martin - 7 years, 9 months ago

How did you get the answer?

Fariz Azmi Pratama - 7 years, 9 months ago

yes.I agree

David L. - 7 years, 9 months ago

tan15=y/x =(2.sin60.t-1/2.10. t^2)/(2.cos60.t)
2-sqrt{3} =sqrt{3}-5t
t={2/5}(sqrt{3}-1)
R= x/sin 15 =t/sin 15 = {4/5}sqrt{2}

Viji Raj - 7 years, 9 months ago

R = x / cos 15

Lokesh Sharma - 7 years, 9 months ago

Yes you are right Lokesh. R=x/cos15 that gives me the same answer as yours

Viji Raj - 7 years, 9 months ago

rotate Oxy 15

gx= -10sin15; gy= -10cos15

t = 2vsin45/gy

R=vcos45t - 1/2 * gx * t^2 =2*(1 - tan15)/cos15

thanh nguyen - 7 years, 8 months ago

We need to start by finding final speed, $v_f$ .

After that, u can start using conservation of mechanical energy

$K_i + U_i = K_f + U_f$

$\frac{1}{2}mv_0{}^{2} = \frac{1}{2} mv_f{}^{2} + mgR\sin 45^{\circ}$

$v_0{}^{2} = v_f{}^{2} + 2gR\sin 45^{\circ}$

Now u have all the values except $R$ and u can easily find $R$

Saad Haider - 7 years, 8 months ago

What is the value of $v_f$ ?

Lokesh Sharma - 7 years, 8 months ago

U can use the equation of kinematics

In the y-direction

$v_{yf}^{2} = (v_0\sin45^{\circ})^{2} -2gR\sin45^{\circ}$

$v_{yf} = v_0\sin 45^{\circ} - gt$

$R\sin 45^{\circ} = v_0\sin 45^{\circ}t - \frac{1}{2} gt^{2}$

$R\sin 45^{\circ} = \frac{1}{2}(v_{yf} + v_0\sin 45^{\circ})t$

In the x-direction

$R\cos 45^{\circ} = v_0\cos 45^{\circ}t$

Using the equations, we can find $v_{yf}$ . We also have $v_{xf} = v_{xi} = v_0\cos 45^{\circ}$ . Then u can find $v_f$ by Pythagoras theorem: $v_f = \sqrt{v_{xf}^{2}+v_{yf}^{2}}$

Saad Haider - 7 years, 7 months ago

i think it would be R=uusin2*/g=0.4m

abhimanyu manu - 7 years, 9 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$