BGN-1.1.1
Note that the definition of trapezoid and trapezium here accord to the American definition.
Formulae 公式
triangles 三角形
Representation of symbols—Image 1.1.1-1
字母含义见图1.1.1-1
Area 面积:
The third line is Heron’s formula, r & R are the in-radius and circumradius of the triangle.
第三行是海龙公式,而 r 和 R 分别是三角形的内接圆和外接圆的半徑。
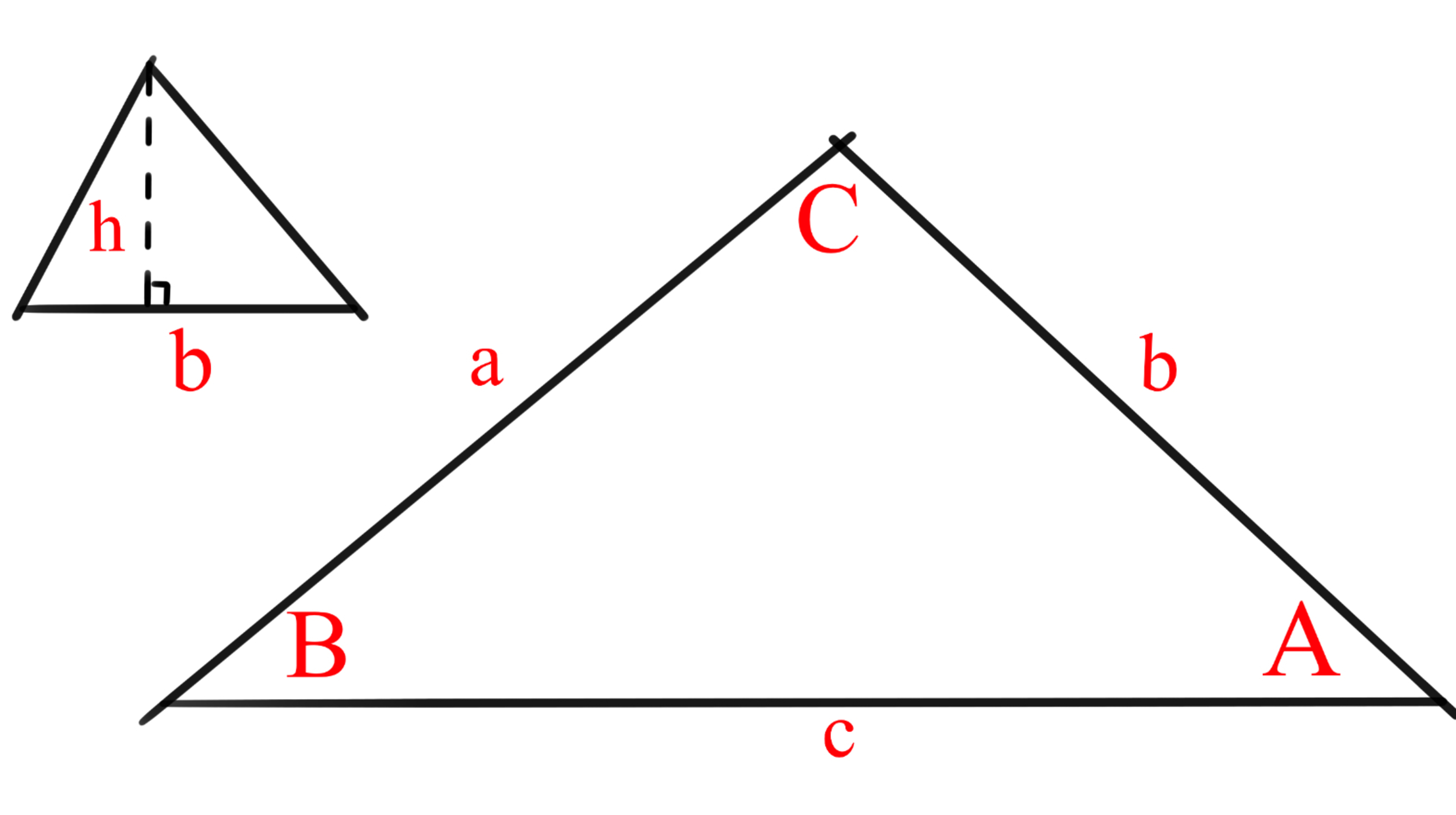 Image 1.1.1-1 图1.1.1-1
Image 1.1.1-1 图1.1.1-1
quadrilaterals 四边形
Representation of symbols—Image 1.1.1-2
字母含义见图1.1.1-2
Square 正方形:
Rectangle 長方形:
Trapezoid 梯形:
Parallelogram 平行四边形: ,
Rhombus 菱形: ,
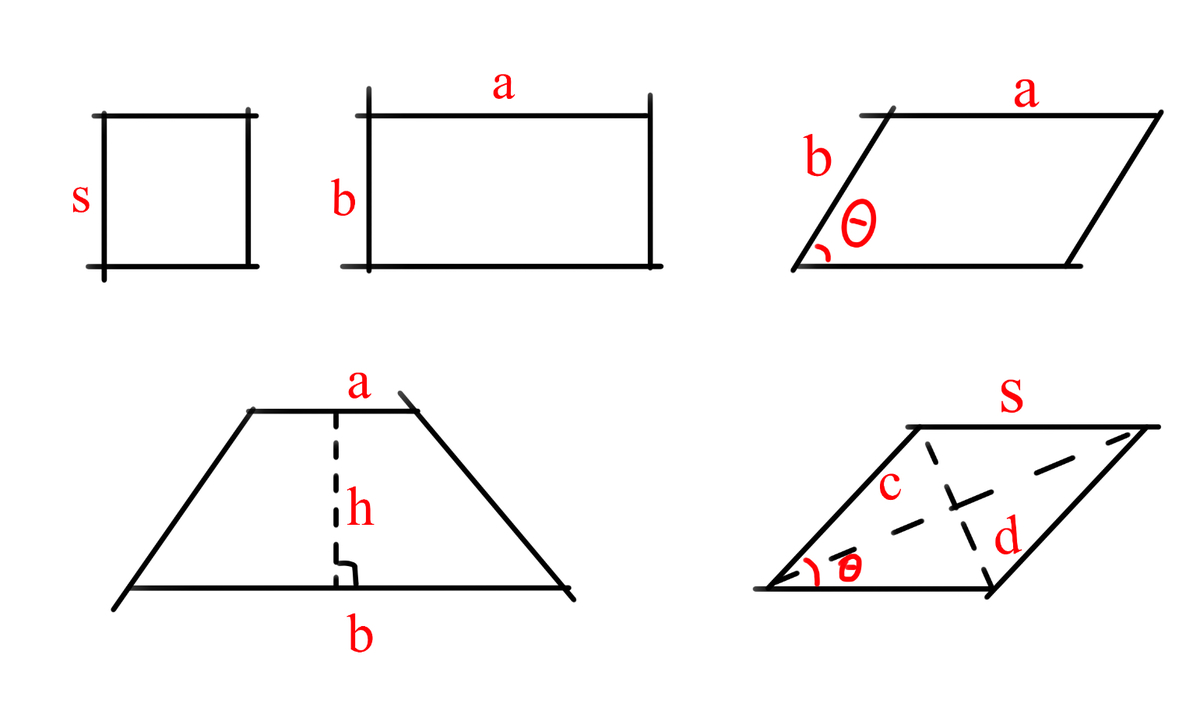 Image 1.1.1-2 图1.1.1-2
P.S. The area of a unit rhombus is equal to and is acute (smaller than ).
Image 1.1.1-2 图1.1.1-2
P.S. The area of a unit rhombus is equal to and is acute (smaller than ).
注:一个边长为1的菱形的面积等于角 的正弦 且角 是锐角。
ellipticals 椭圆形
Circle 圆: , where is the radius. , 代表半径。
Oval 椭圆: , where is half the long axis, is half the short axis. , 分别指长轴的一半和短轴的一半。
Proof 证明
quadrilaterals 四边形
Imagine a rectangle grid (chocolate bar) with rows and columns of unit grids (squares of side length 1 unit). It will have rows of length , i.e. rows of area , so it’s size is
Same for squares.
想象一个有a行,b列的长方形网格(或植物大战僵尸场地)。它有a个b格长的列,即a个面积为b的列,所以其面积为
正方形同理。
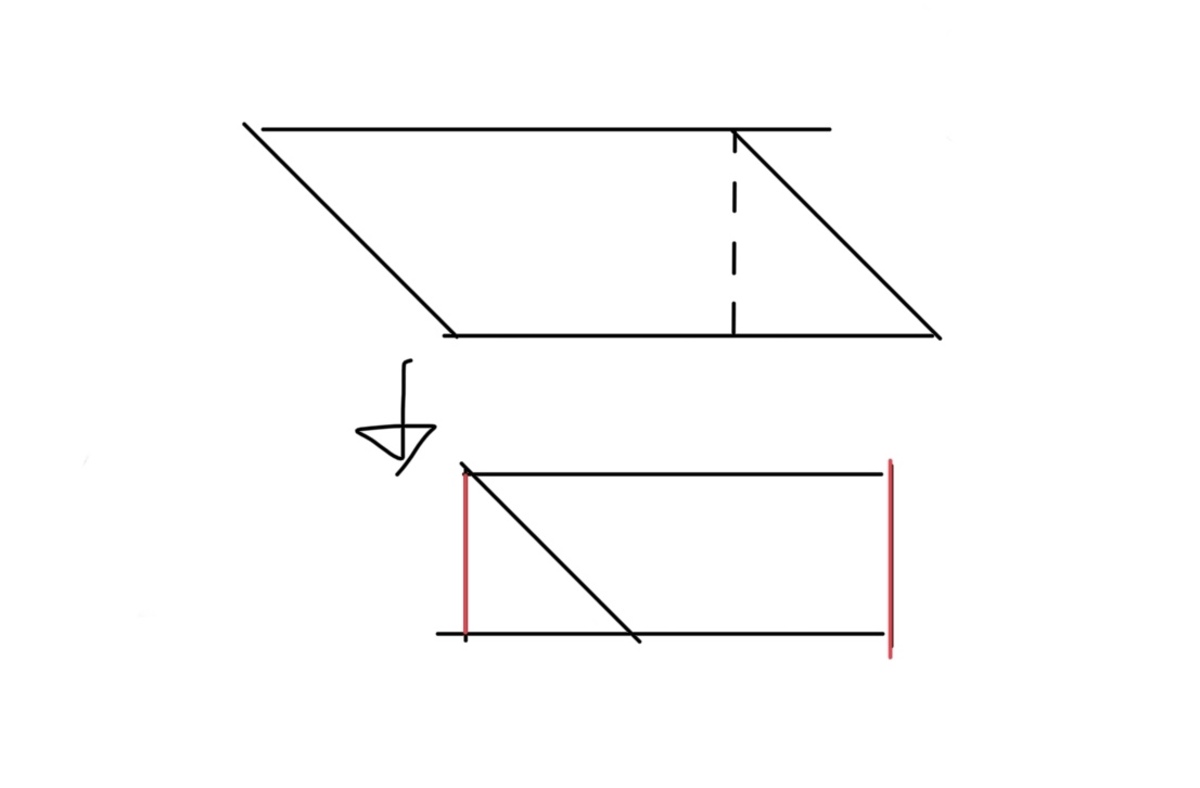 Image 1.1.1-3 图1.1.1-3
Image 1.1.1-3 图1.1.1-3
As for parallelograms (including rhombuses), we can split them into two like this
so it’s area is .
对于平行四边形(和菱形),可以拼切成长方形处理(如右图),得面积公式为 。
Two identical trapezoids can be put together to form a parallelogram with base , height , so one trapezoid has size .
两个全等的梯形可以拼合成一个底为 ,高为 的平行四边形,所以一个梯形的大小就是 。
The other formulae of quadrilaterals mentioned above will not be specifically explained, but you can check the wiki and solve yourself. 其他四边形的上述公式不在此详解,如有兴趣可自行推导。
triangles 三角形
Most triangle size formulae are given by half the size formulae of parallelograms.
ellipticals 椭圆形
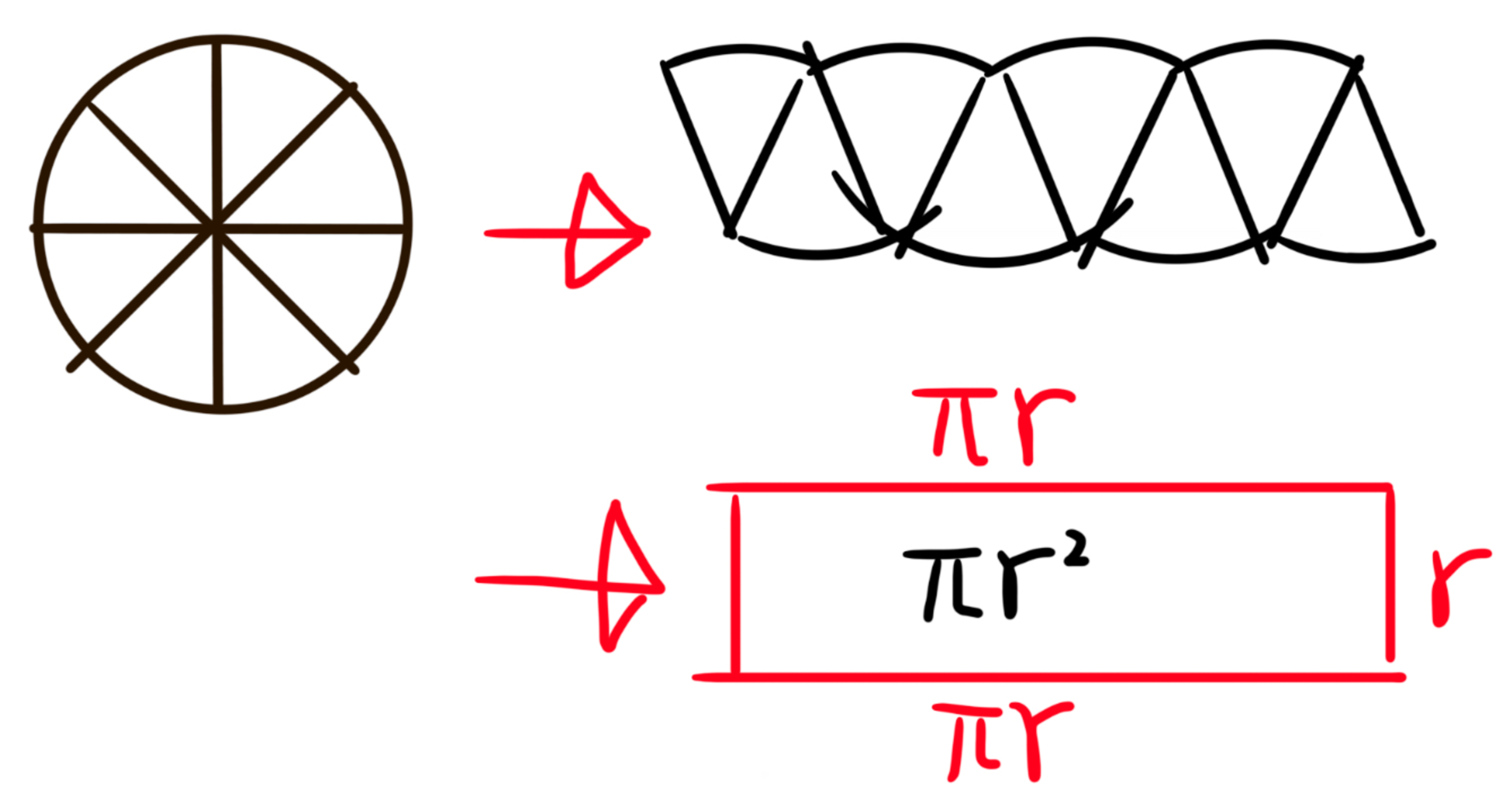 Image 1.1.1-4 图1.1.1-4
Split a circle into equal pieces. Arranging, we get a ‘rectangle’. The more pieces the circle is split in, the more close the arranged shape is to a rectangle with base , height .
Image 1.1.1-4 图1.1.1-4
Split a circle into equal pieces. Arranging, we get a ‘rectangle’. The more pieces the circle is split in, the more close the arranged shape is to a rectangle with base , height .
将一个圆形分成全等的几份。重新拼接后,我们可以得到一个近似长方形。当圆形被分成的份数增加,拼接后的图形就会趋向于一个底为 ,高为 的长方形。
Techniques 技巧
For other polygons, you can either split them up or think of them as a few small polygons taken from a big one.
对于其他多边形,我们可以将其视为一些图形的结合或一个被裁减的大多边形。
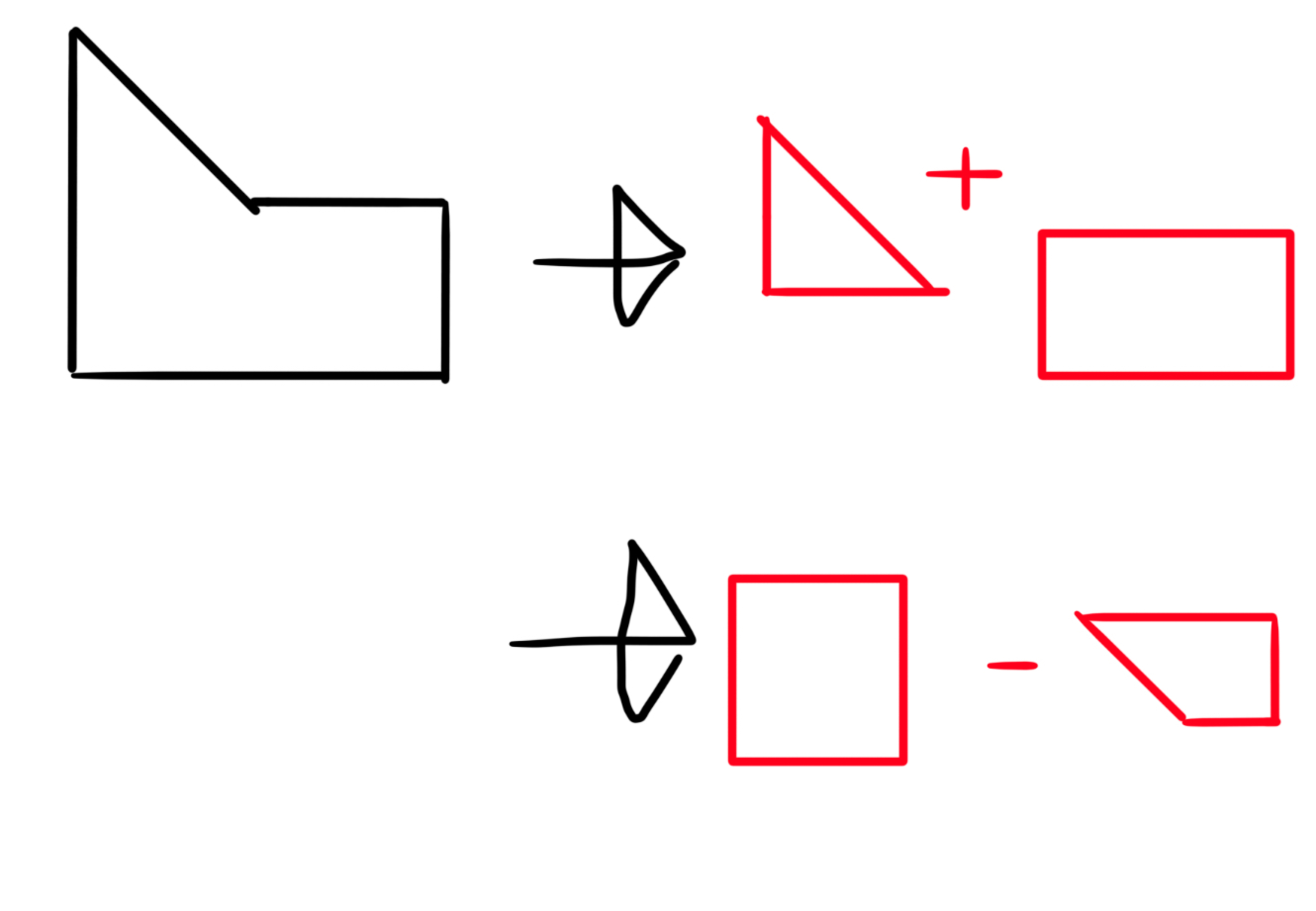 Image 1.1.1-5 图1.1.1-5
Image 1.1.1-5 图1.1.1-5
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
Put this one and the Bilingual Geometry Notebook in your RadMaths note!
Log in to reply
Yup, working on that
Report to moderators:
 This happened when I tried to edit my OTHER note but forgot to close a LaTeX bracket. Then the note malfunctioned and no matter how I refreshed my browser it still showed up wrong. :( Please help! 🙏
This happened when I tried to edit my OTHER note but forgot to close a LaTeX bracket. Then the note malfunctioned and no matter how I refreshed my browser it still showed up wrong. :( Please help! 🙏
@Brilliant Mathematics
Log in to reply
@Brilliant Mathematics
Hi Jeff, this page looks fine by me. Do you still face the same issue?
Log in to reply
THIS page is fine, but it’s my OTHER page that malfunctioned :)
Log in to reply
Hi Jeff, the other pages look fine by me as well.
Please send me the relevant URL of your notes that have been affected. Thank you.
Log in to reply
I know:
BGN-1.1.2