Bound Charge at Dielectric Interface

Here is a question sent to me recently:

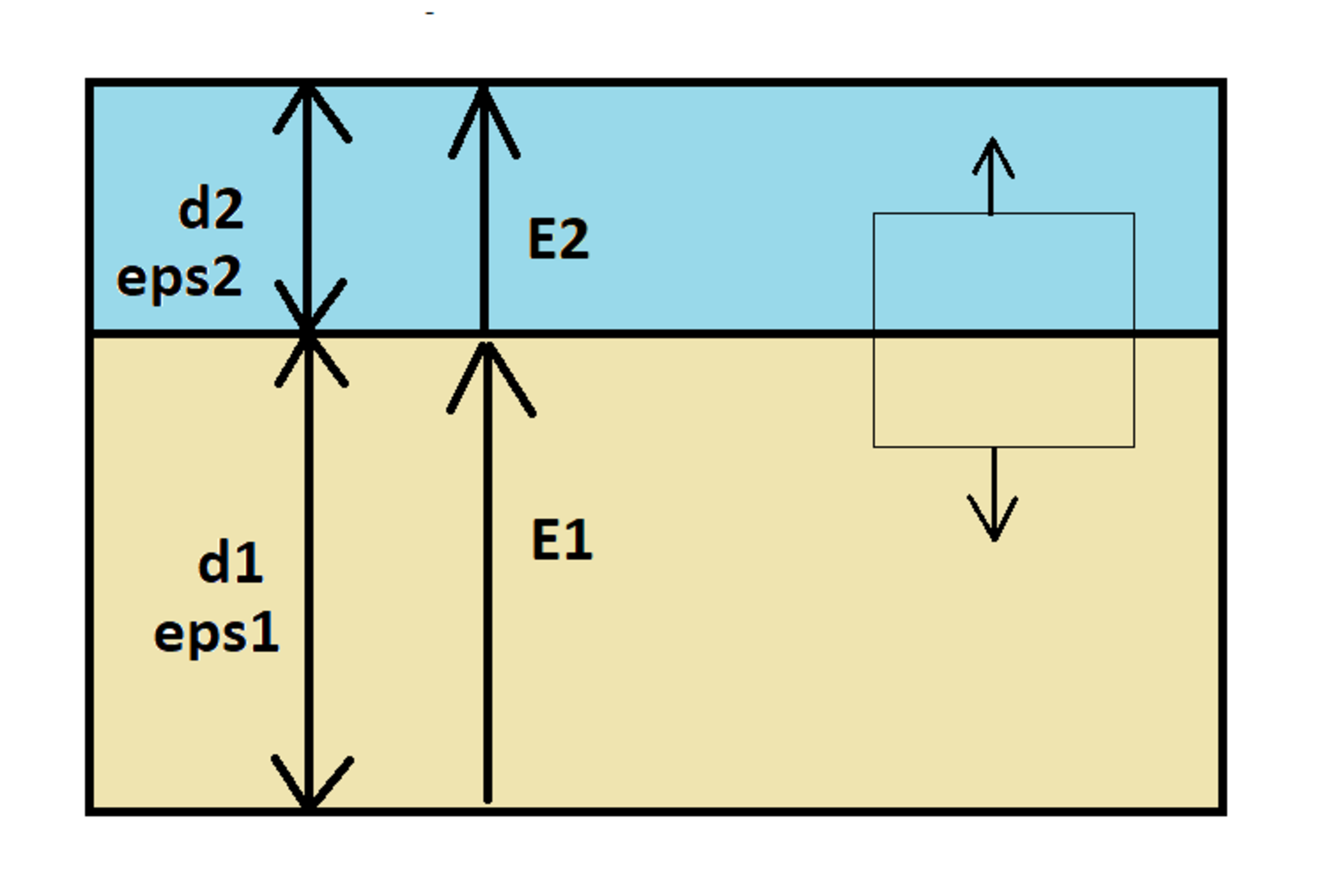
I will look at part (b). Let $\epsilon_1$ and $\epsilon_2$ be the relative electric permittivity values. The field continuity equation is (where the electric fields are perpendicular to the interface boundary):

$\epsilon_1 E_1 = \epsilon_2 E_2$

Relate the voltage across the capacitor to the electric fields:

$V = E_1 d_1 + E_2 d_2 = E_1 \Big(d_1 + \frac{\epsilon_1}{\epsilon_2} d_2 \Big) \\ E_1 = \frac{V \epsilon_2}{d_1 \epsilon_2 + d_2 \epsilon_1} \\ E_2 = \frac{V \epsilon_1}{d_1 \epsilon_2 + d_2 \epsilon_1}$

Consider the Gaussian surface shown to the right within the dielectric. The formula for bound charge at a dielectric interface is similar to the formula for Gauss's Law, but with a slight variation. Surfaces $S_2$ and $S_1$ are the top and bottom Gaussian sub-surfaces.

$Q_b = (\epsilon_1 - 1) \epsilon_0 \int \int_{S1} \vec{E}_1 \cdot \vec{dS_1} + (\epsilon_2 - 1) \epsilon_0 \int \int_{S2} \vec{E}_2 \cdot \vec{dS_2}$

Note that the normal vector for $S_1$ points in the opposite direction as the electric field, and the normal vector for $S_2$ points in the same direction as the electric field. Let these surfaces both have area $S$. The equation simplifies to:

$Q_b = (\epsilon_1 - 1) \epsilon_0 (- E_1 S) + (\epsilon_2 - 1) \epsilon_0 (E_2 S)$

Applying the field continuity relationship makes the relative permittivity terms disappear.

$Q_b = \epsilon_0 (E_1 S) - \epsilon_0 (E_2 S)$

Dividing both sides by $S$ gives the bound charge density:

$\sigma' = \epsilon_0 E_1 - \epsilon_0 E_2 = \epsilon_0 \Big( \frac{V \epsilon_2 - V \epsilon_1}{d_1 \epsilon_2 + d_2 \epsilon_1} \Big)$