[Brilliant Blog] Lunar Eclipses and the Scale of the Sun and Moon

Main post link -> http://blog.brilliant.org/2013/01/13/lunar-eclipses-and-the-scale-of-the-sun-and-moon/

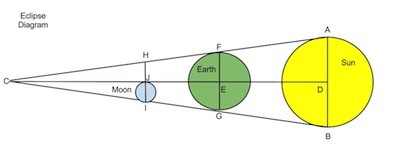
...(Read the full method on the blog) Using his low estimate as an example, this is how he calculated the sizes and distances of the Sun and Moon, in Earth radii(e.r.):

$\frac{AB}{JI} = \frac{18}{1}$

$HI = 2JI$

That would make $HI$ $\frac{1}{9}$ of $AB$. By the similarity of triangles $ACB$ and $HCI$, that would make the distance of $DC$ 9 times greater than $JC$.

$\frac{HI}{AB} = \frac{1}{9}$

$\frac{DC}{JC} = \frac{9}{1}$

From this, $\frac{DC}{DJ}$ would be $\frac{9}{8}$. If the Sun is 18 times further away from the Earth than the Moon is, when the Moon is on the opposite side of the Earth from the Sun, it is an additional $\frac{1}{18}$ the Earth-Sun distance from the Sun. So:

$\frac{DC}{DJ} = \frac{9}{8}$

$\frac{DJ}{DE} = \frac {19}{18}$

What he wanted was the ratio of $\frac{DC}{DE}$ so that by comparing similar triangles he could get $\frac{AB}{FG}$. From the relationships above:

$DC = DJ \frac{9}{8}$

$DE = DJ \frac{18}{19}$

$\frac{DC}{DE} = \frac{9\times19}{8\times 18} = \frac{19}{16}$

From the similarity of triangles $ACB$ and $FCG$ he found the Earth to be at most $\frac{3}{19}$ the size of the sun and about 3 times larger than the moon(60/19).