Calculus + Factorial = ?

Recently, I've been messing around with factorials (mainly because I was just told that $x! \approx (\frac{x}{e})^x\times\sqrt{2\pi x}$ ). I came across a couple calculus problems involving the function. Since I am very new to calculus, I figured I should ask the community on how to get the answers and what they are, not just by typing them into Wolfram Alpha and seeing what comes out.

Since $x!$ increases so rapidly, I decided taking the $x$ root of $x!$ . This gave me the function, $\color{#D61F06}{f(x)=x!^{\frac{1}{x}}}$ . That function is the red graph in the picture below.

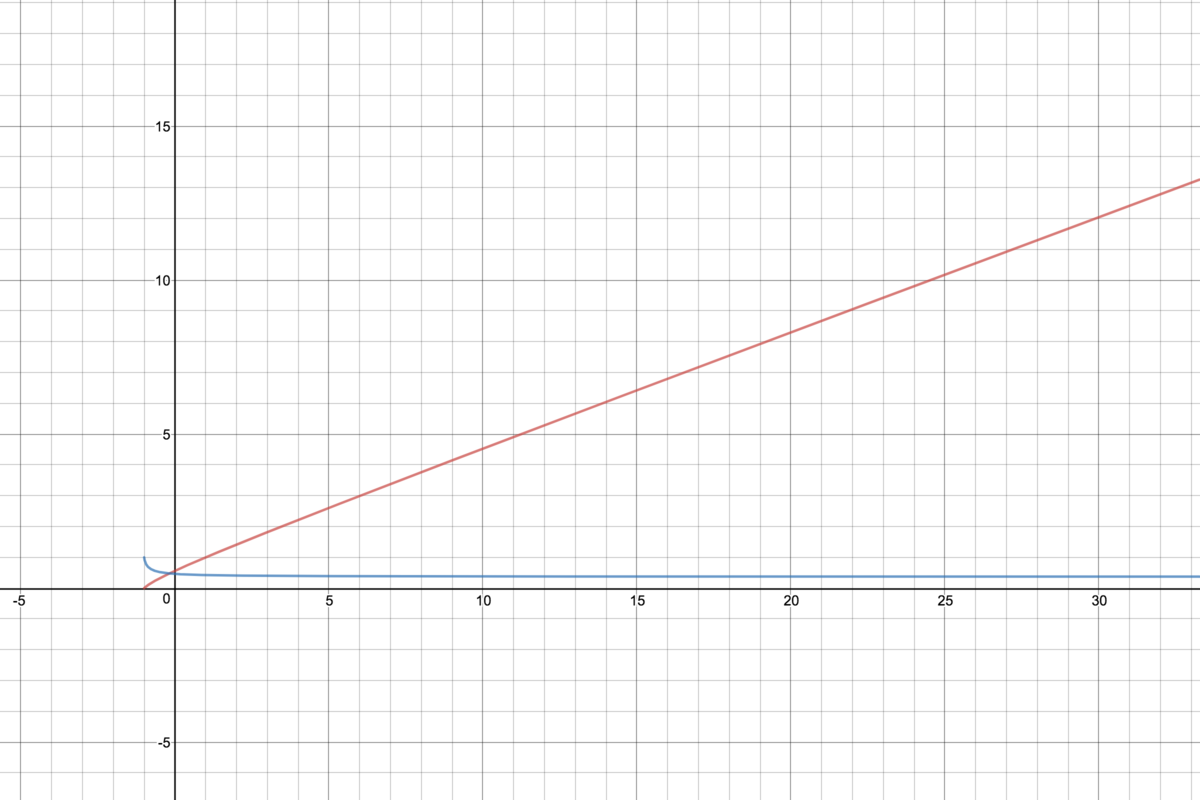
I noticed that, even though $f(0)$ is undefined (since $\frac{1}{0}$ is undefined), it still appears to have a value. That is my first problem: to find

$\lim_{x\rightarrow 0} \color{#D61F06}{f(x)}$

Next, I noticed that $\color{#D61F06}{f(x)}$ is not linear. However, it appeared to be linear, so I decided to graph the derivative, which gave me the function $\color{#3D99F6}{g(x)=\dfrac{\text{d}}{\text{d}x}~f(x)}$ . This is the blue graph in the picture above. Since $\color{#D61F06}{f(x)}$ approached linearity (?), I knew that $\color{#3D99F6}{g(x)}$ must have a limit as it approached infinity. That leads me to my second problem: to find

$\lim_{x\rightarrow \infty} \color{#3D99F6}{g(x)}$

The graph is at this link.

NOTE: The domains of both functions stop before 171 because 171! is a massive number, to the point that most online calculators can't handle.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Stirling's formula is a good reference for the approximation. Note that this approximation holds for large values, and not necessarily for small values.
According to Wolfram Alpha, $\lim_{x\rightarrow 0 } f(x)$ is an interesting value.
It is not immediately apparant to me why this is true as yet.
Note: $\gamma$ is the Euler-Mascheroni constant.
Note that $f(x) \approx \frac{x}{e}$ for larget values. Hence, if there is any justice in the world (meaning that if the limit exists), it is most likely that $\lim g(x) = \frac{1}[e}$ .
However, there is a slight flaw in your logic. Namely, the following statement is not true: "If $| f(x) - g(x) | < \epsilon$ for all $x$ , then $\lim g'(x) = \lim f'(x)$ .".
An extra condition will need to be added to arrive at "If $f(x) \approx g(x)$ (in some manner), then $\lim g'(x) = \lim f'(x)$ ."

Calvin Lin Staff - 3 years, 3 months ago

$\displaystyle L=\lim_{n\to 0} (n!)^{\frac 1n}=\lim_{n\to 0} (\Gamma(n+1))^{\frac 1n}$ $\displaystyle L=\lim_{n\to 0} e^{\frac {\ln (\Gamma(n+1))}{n}}=e^{\lim_{n\to 0} \frac {\ln(\Gamma(n+1))}{n}}$

Using L'Hospital rule we get $\displaystyle L= e^{\lim_{n\to 0} \psi(n+1)}=e^{\psi(1)}$

And using $\psi(1)=-\gamma$ we get $L=e^{-\gamma}$

Where $\Gamma(.)$ is the Gamma function, $\psi(z)$ is the Digamma function and $\gamma$ is the Euler-Mascheroni constant

Rohan Shinde - 2 years, 3 months ago

I did some experimenting with factorials, here are some interested facts:

The limit as f(x) approaches 0 is equal to the negative root of the equation $x!=2$
The limit as g(x) approaches infinity is equal to this limit: $\large \lim_{x \to \infty}(x^{0.1}e^{-x})^{\frac{1}{x}}$ and also this limit: (x can be any postive real number) $\large \lim_{n \to 0}(x^{n}e^{-x})^{\frac{1}{x}}$

Those limits are derived from the gamma function, and the second one seem to evaluate to $\frac{1}{e}$

Anthony Xu - 3 years, 2 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$