Can You Help ?

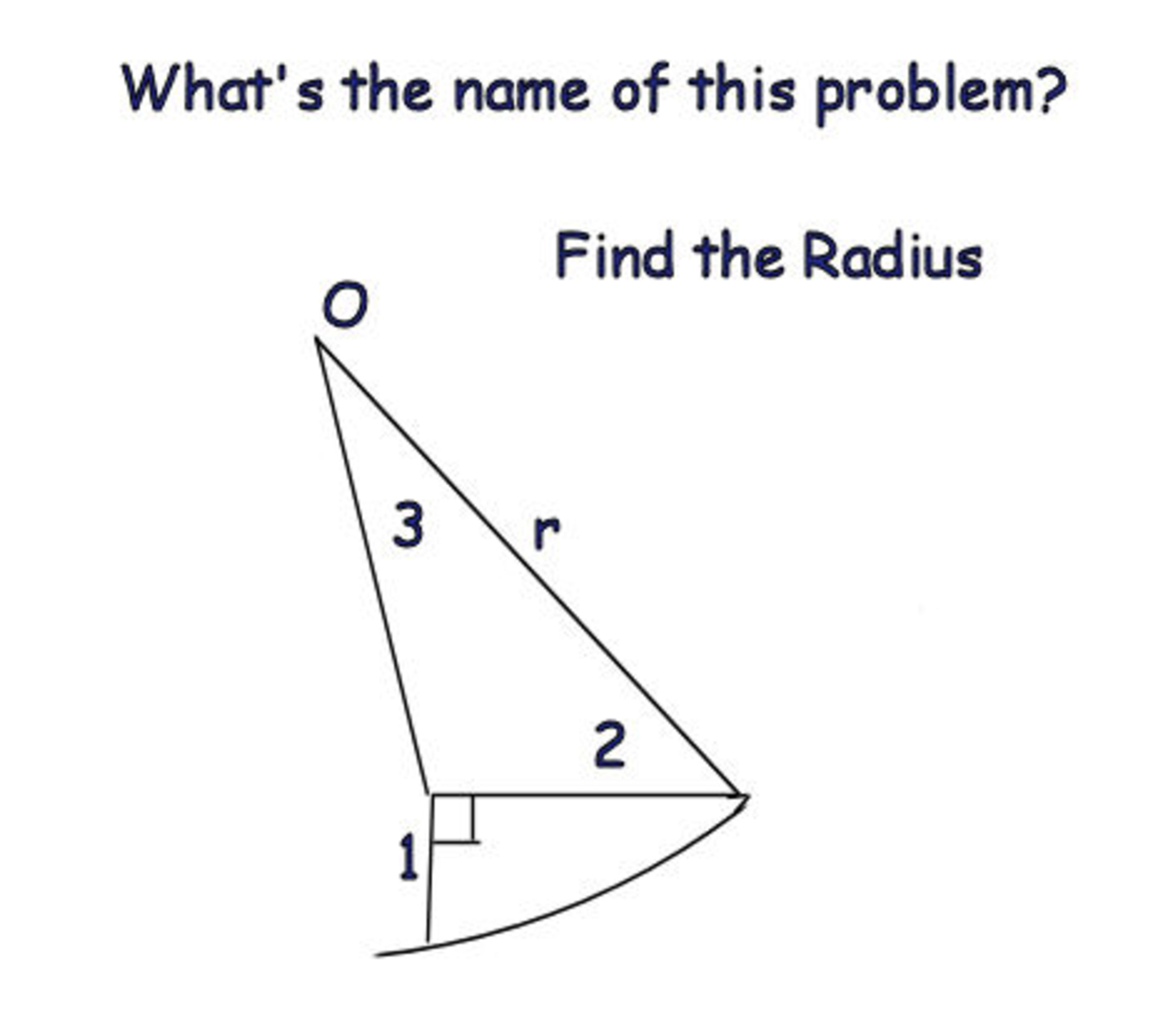
Please help me identify a problem I was working on.

I usually save the interesting ones in a set for future examination but I didn't this time and I think I'm on the way to solving it.

This is the setup:

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

I'm getting a value of $r = \displaystyle\sqrt{\dfrac{53 + 6\sqrt{19}}{5}}$ ,

which equals $3.9788$ rounded to $4$ decimal places. Is that what you got? I'll write up my method shortly.

Edit: Label the triangle so that $OA = 3$ and $AB = 2$ . Also, label the length $1$ line segment $AP$ and let $\angle OAB = \theta$ .

Then $OP = r$ and $\angle OAP = \frac{3\pi}{2} - \theta$ . We can now apply the Cosine Law to triangles $\Delta OAB$ and $\Delta OAP$ to obtain the equations

(i) $r^{2} = 3^{2} + 2^{2} - 2*3*2*\cos(\theta) \Longrightarrow 13 - 12\cos(\theta)$ , and

(ii) $r^{2} = 3^{2} + 1^{2} - 2*3*1*\cos(\frac{3\pi}{2} - \theta) \Longrightarrow 10 + 6\sin(\theta)$ .

Equating (i) and (ii) we then have that

$13 - 12\cos(\theta) = 10 + 6\sin(\theta) \Longrightarrow 1 - 4\cos(\theta) = 2\sin(\theta)$ .

Now square both sides and simplify to find that

$1 - 8\cos(\theta) + 16\cos^{2}(\theta) = 4*(1 - \cos^{2}(\theta)) \Longrightarrow 20\cos^{2}(\theta) - 8\cos(\theta) - 3 = 0$ ,

which has solutions $\cos(\theta) = \dfrac{8 \pm \sqrt{64 + 4*3*20}}{2*20} = \dfrac{1}{5} \pm \dfrac{\sqrt{19}}{10}$ .

Now from the diagram we are looking for $\theta \gt \frac{\pi}{2}$ , i.e., $\cos(\theta) \lt 0$ , se we take the root

$\cos(\theta) = \dfrac{1}{5} - \dfrac{\sqrt{19}}{10}$ .

Now substitute this value into (i) to find that

$r^{2} = 13 - 12*(\dfrac{1}{5} - \dfrac{\sqrt{19}}{10}) = \dfrac{53 + 6\sqrt{19}}{5}$ ,

and so $r = \displaystyle\sqrt{\dfrac{53 + 6\sqrt{19}}{5}}$ .

Brian Charlesworth - 6 years, 6 months ago

Hi, Brian, what's the name of the problem?

Guiseppi Butel - 6 years, 6 months ago

Oh, sorry, you were just wanting a name. I have no idea if it has a specific name, but it seems to be an exercise in the application of the Cosine Law. I can think of one other way of trying to solve it, but I haven't worked out the details of that approach yet.

I'm sorry if I spoiled this question for posting. I just saw it as an interesting problem and immediately had to solve it. You could delete this note and then post the problem after; I would be fine with that. :)

Brian Charlesworth - 6 years, 6 months ago

Uh oh, answer spoiled? D:

Daniel Liu - 6 years, 5 months ago

Yeah, I know. I don't think it's a big problem, since this posts has no likes or re-shares. Sorry about this; I had no idea about the question's "history" at the time I posted my solution. :(

Brian Charlesworth - 6 years, 5 months ago

@Brian Charlesworth – Nah, it's fine. You also forgot to prove that $\theta > \dfrac{\pi}{2}$ , although it may be obvious.

Daniel Liu - 6 years, 5 months ago

@Daniel Liu – O.k., I'm glad. And yes, I did gloss over that detail, and even though it does seem obvious it would require a proof. At this stage, though, I'm just going to stick with "And clearly, $\theta \gt \dfrac{\pi}{2}$ ". :)

Brian Charlesworth - 6 years, 5 months ago

I think I did see this problem somewhere else posted in Brilliant, but I can't think of the name of either the problem or the creator. Brian's answer is correct, though.

Okay, I've found the problem, posted by [Deleted]

[Deleted]

Michael Mendrin - 6 years, 6 months ago

Well, that made it easy for me to solve [deleted]'s question, then. :) Having found a solution assuming that $\theta$ was obtuse it is clear that $\theta$ can be obtuse, but I neglected to prove that $\theta$ would necessarily have to be obtuse. I see that in response to [deleted]'s solution to his own problem, Ariel Gershon has proved this to be the case.

Brian Charlesworth - 6 years, 6 months ago

lol free rating...

math man - 6 years, 6 months ago

@Math Man – Yeah, I know. I wonder if I should delete my answer now. I had no idea the question had been asked on Brilliant before until Michael posted the link. It's not fair to [deleted] if people can now cheat on his question, but Guiseppi asked this question independently so I don't want to delete my answer to his question.

Brian Charlesworth - 6 years, 6 months ago

@Brian Charlesworth – i dont know.... , i think u should delete it.

math man - 6 years, 6 months ago

@Math Man – Problem solved. No more free points. :)

Brian Charlesworth - 6 years, 6 months ago

@Brian Charlesworth – lol

no free shot to lv5 geometry attempt

math man - 6 years, 6 months ago

@Brian Charlesworth – without it, i will never solve it

math man - 6 years, 6 months ago

Hi Michael. In light of Math Man's comment below, I'm wondering if it's a good idea having the link to [deleted]'s question posted here. whatever you decide is fine, but I just thought I should give you a heads up. I could delete my answer, but then that would defeat the point of Guiseppi's post.

Brian Charlesworth - 6 years, 6 months ago

Okay, deleted, as I noticed that problem has just now been reshared.

Michael Mendrin - 6 years, 6 months ago

@Michael Mendrin – Thanks, Michael. I've inserted a few [deleted]'s as well.

Brian Charlesworth - 6 years, 6 months ago

its title is this: [deleted]

Moderator's note: please do not post spoilers

Rudresh Tomar - 6 years, 4 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$