Can you prove this?

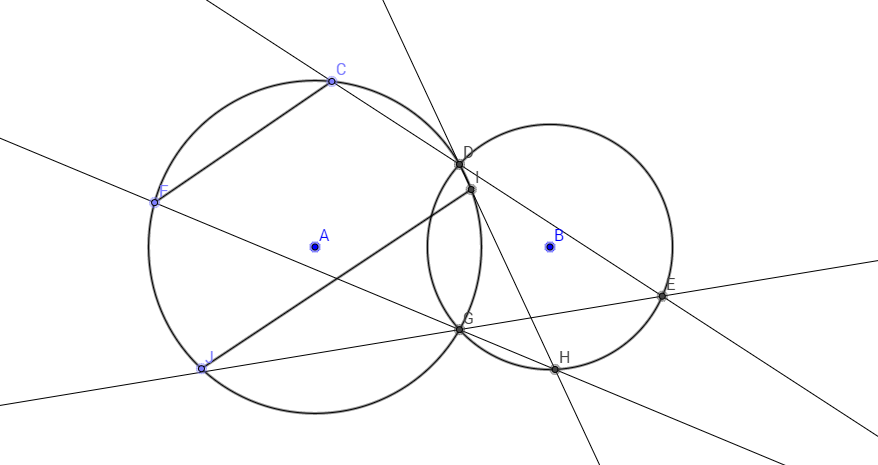There are two intersecting circles G1 and G2 with centres at A and B respectively. They meet at points D and G. You choose any two points C and F on the cirle G1. From C, you draw a line through D to meet G2 at E. Through E, draw a line passing through G to meeet G1 at J. Now, you draw a line from F through G to meet G2 at H. From H, you draw a line through D to meet the circle circle at I. Connect C and F amd I and J. Prove that IJ is parallel to CF.

This figure is part of the solution:

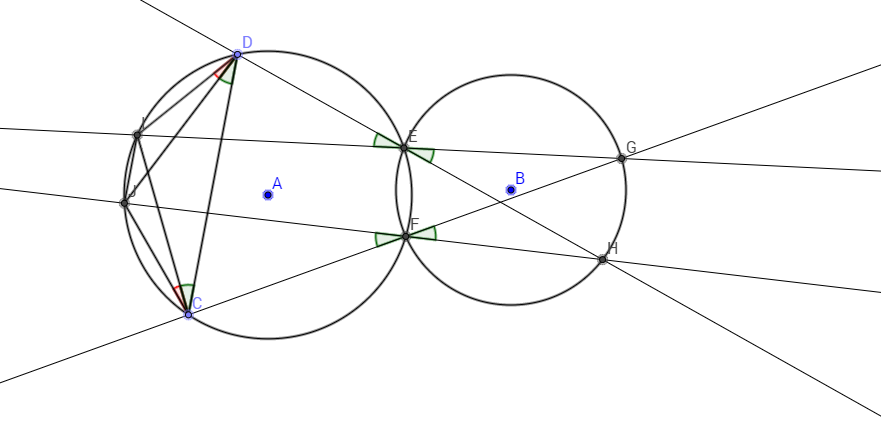
I changed the label of F to D. So now, it's prove that CD is parallel to IJ. Start out with angle JCI, which is equal to angle JDI. So now, we only have to show that angle JDC is equal to angle ICD and we get an isosceles trapezium CDIJ and we're done. Angle JDC is equal to angle JFC which is equal to HFG which is equal to angle HEG, which is equal to angle IED which is equal to angle ICD.

Q.E.D.

If you want a more challenging version of this, then checkout my problem here

#Geometry

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

This is just a quick hunch, given two such circles G1 and G2 intersecting at points D, G, given any point E on G2, and extending lines ED and EG to meet G1 at points C and J, the chord length of CJ is constant. The rest of the proof follows.

I'll back to this a little later with maybe a graphic to show this.

Okay, here's the graphic. With a bit of angle chasing, it's easy to show that, given angles $a, b$ formed by two intersecting circles, for any $x$ formed by arbitrary point $E$ , the angle subtended by chord $CJ$ is $a+b$ . Therefore, the length of chord $CJ$ is constant for any $E$ . With this, it's straightforward to show that $IJ$ is parallel to $GF$ .

Michael Mendrin - 6 years, 1 month ago

Wow! Really awesome proof. This question is not original and is from last year's entrance exam to a college over here. I couldn't solve it when I was going through the paper yesterday. I too tried to relate it to an isosceles trapezium, but I gave up. I had to look up the solution to this question to get the method.

Their method made it seem so simple that I felt like smacking myself in the head. I have a figure that I'll post which makes it really obvious. I changed the labels, so now it's prove that CD is parallel to IJ.