Can you solve it?

Hi guys,

can you solve this puzzle??

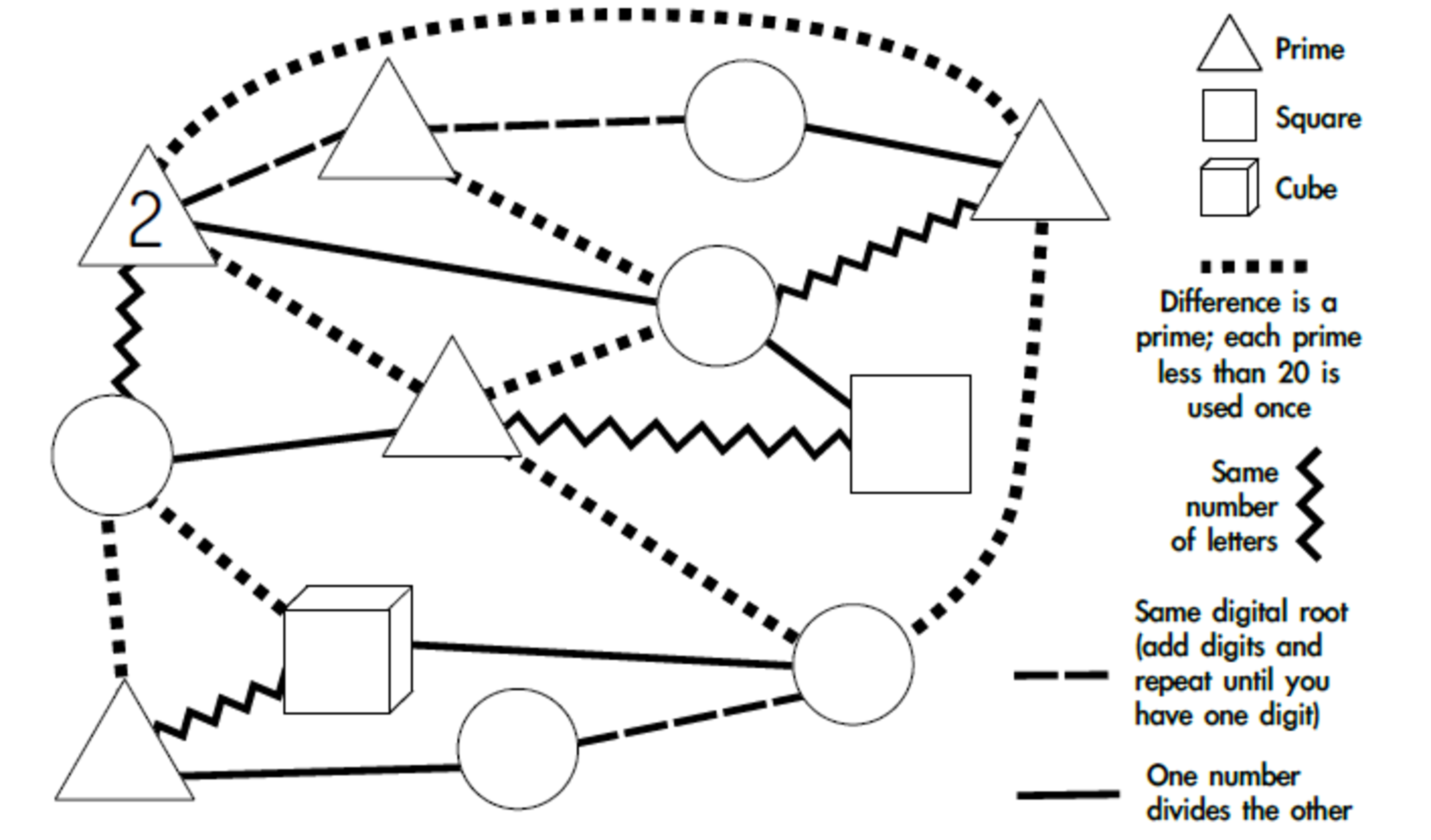
The numbers to fit in are:

$\boldsymbol \not{2},3,5,8,9,10,18,19,24,29,33,38$

Try to solve it and compare with The solution

#TrialAndError #Numbers #Logic #Logicalreasoning #Puzzles

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Hi, I'm not sure if this problem can be solved. Here are my steps, and please correct me if you spot an error (since my Math is quite noob) Filling in the most "obvious" blanks, the square has to be 9 since 9 is the only perfect square in the list. Based on this, the triangle next to the square has to be equal to either 3 or 5, since they are both single-digit numbers (I'm assuming that the "letters" mean "digits"). Checking again, the difference between 5 and 2 is a prime number (3) which fits the requirements. However, the only multiple of 5 in the list (excluding 5 as it has been used) is 10. Hence 10 has to go in the circle on the left of the triangle. There is a contradiction as 10 is a 2-digit number while 2 is a one-digit number? Have I made a mistake somewhere? >.<

Nicole Tay - 5 years, 10 months ago

There is no contradiction because letters mean letters so the number of letters of $10$ are $3$ and same for $2$

Abdeslem Smahi - 5 years, 10 months ago

Oh I see. So "letters" here means the number of letters in the spelling of the number...

Nicole Tay - 5 years, 10 months ago

@Nicole Tay – Yes that's it

Abdeslem Smahi - 5 years, 10 months ago

@Abdeslem Smahi – Great! I've gotten the same answer as in the solution.

Nicole Tay - 5 years, 10 months ago

2, 29, 38, 19, 10, 5, 18, 9, 8, 3, 33 and lastly 24 are placed left to right ( a la reading-style) and found in the same order easily.

Rajen Kapur - 5 years, 10 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$