Capacitor Charge Problem

Here is a question shared by Neeraj.

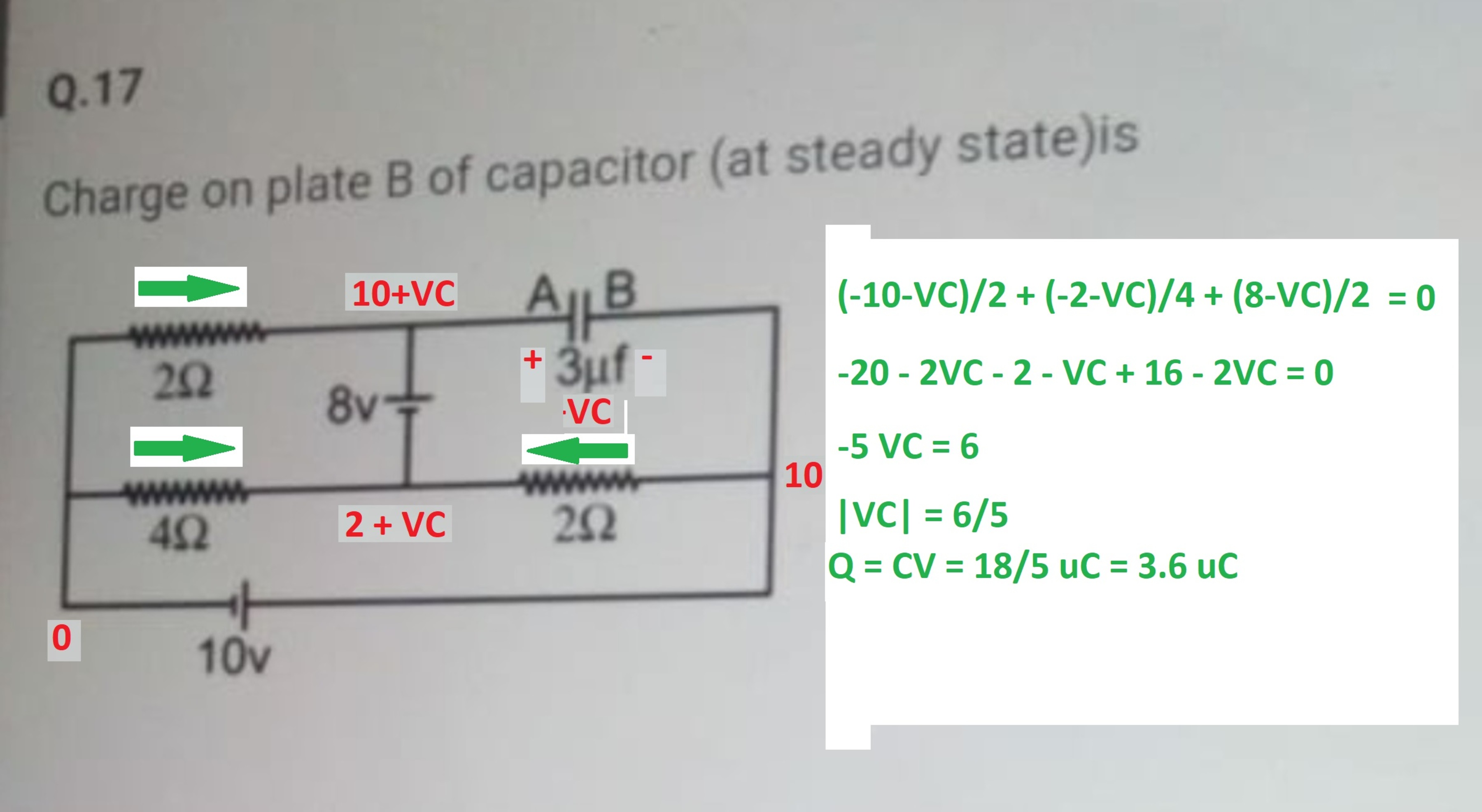
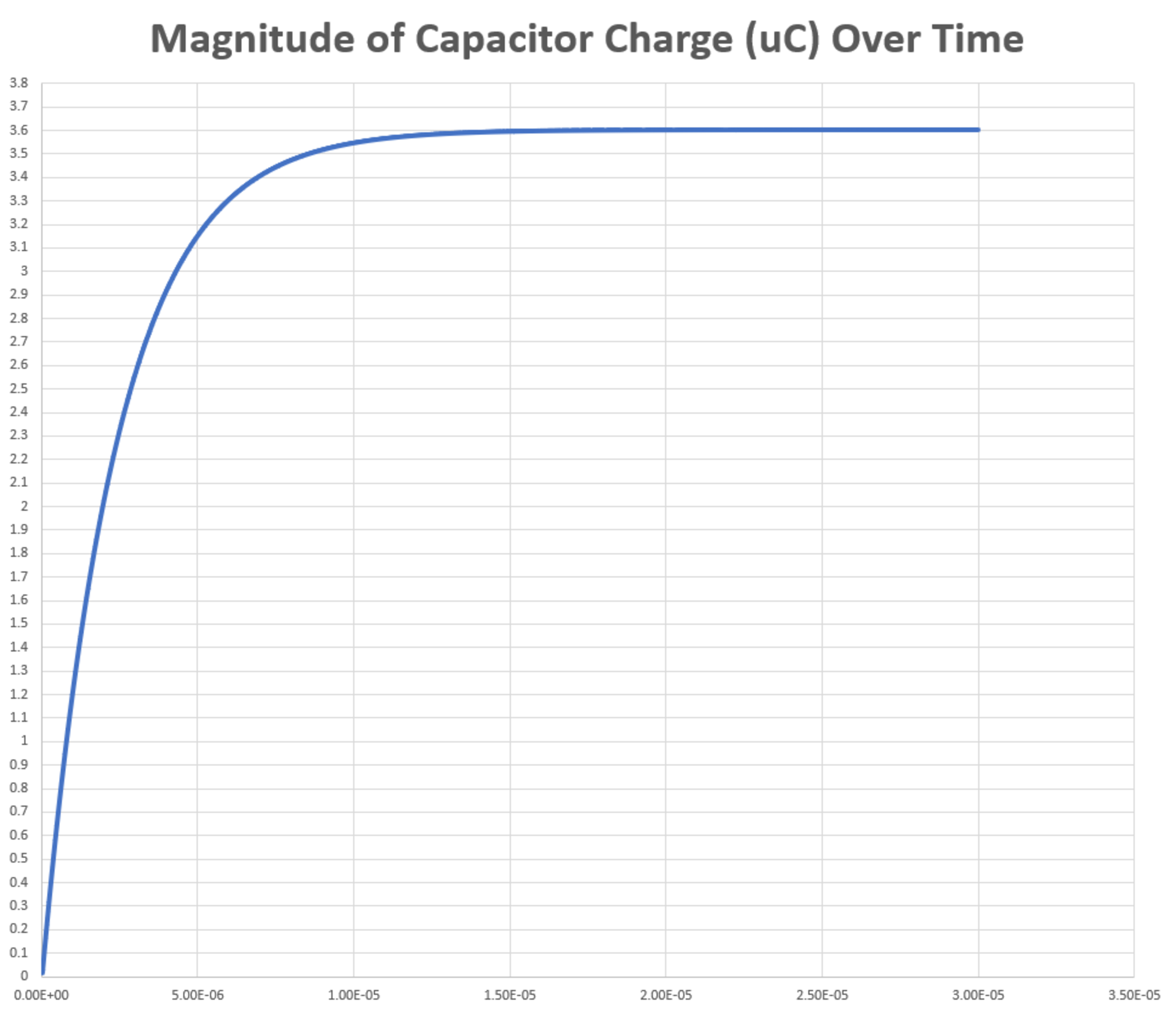
I have included in the image the analysis necessary to determine the steady state capacitor charge magnitude. The Python code below uses numerical integration to compute the evolution of the capacitor charge over time. Within about 20 microseconds, the code solution converges to the known steady state solution.

import math

dt = 10.0**(-9.0)

u = 10.0**(-6.0)

C = 3.0*u

######################################

t = 0.0
count = 0

VC = 0.0

I1 = (0.0 - (10.0+VC))/2.0
I2 = (0.0 - (2.0+VC))/4.0
I3 = (10.0 - (2.0+VC))/2.0

IC = I1 + I2 + I3
# IC = C*VCd

VCd = IC/C

while t <= 30.0*u:

    VC = VC + VCd*dt

    I1 = (0.0 - (10.0+VC))/2.0
    I2 = (0.0 - (2.0+VC))/4.0
    I3 = (10.0 - (2.0+VC))/2.0

    IC = I1 + I2 + I3
    # IC = C*VCd

    VCd = IC/C

    Q = C*VC

    t = t + dt
    count = count + 1

    if count%10 == 0:
        print t,(abs(Q)/u)

#ElectricityAndMagnetism

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

@Lil Doug

Steven Chase - 10 months, 1 week ago

Yeah Very nice, I wanted this method only. Maybe this is long but its crazy.
Thank you so much.

Talulah Riley - 10 months, 1 week ago

You're welcome. What is long?

Steven Chase - 10 months, 1 week ago

@Steven Chase The code is long for me. Maybe for you not because you are a experienced LPE.
Thanks again .

Talulah Riley - 10 months, 1 week ago

@Talulah Riley – Yeah, I think it took me about 3 minutes

Steven Chase - 10 months, 1 week ago

@Steven Chase – @Steven Chase it will take me minimum 10 min to type this code. You are a legend ,smart and stud.

Talulah Riley - 10 months, 1 week ago

@Steven Chase try the 45th problem

Talulah Riley - 10 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$