Chutes and Ladders Programming Problem

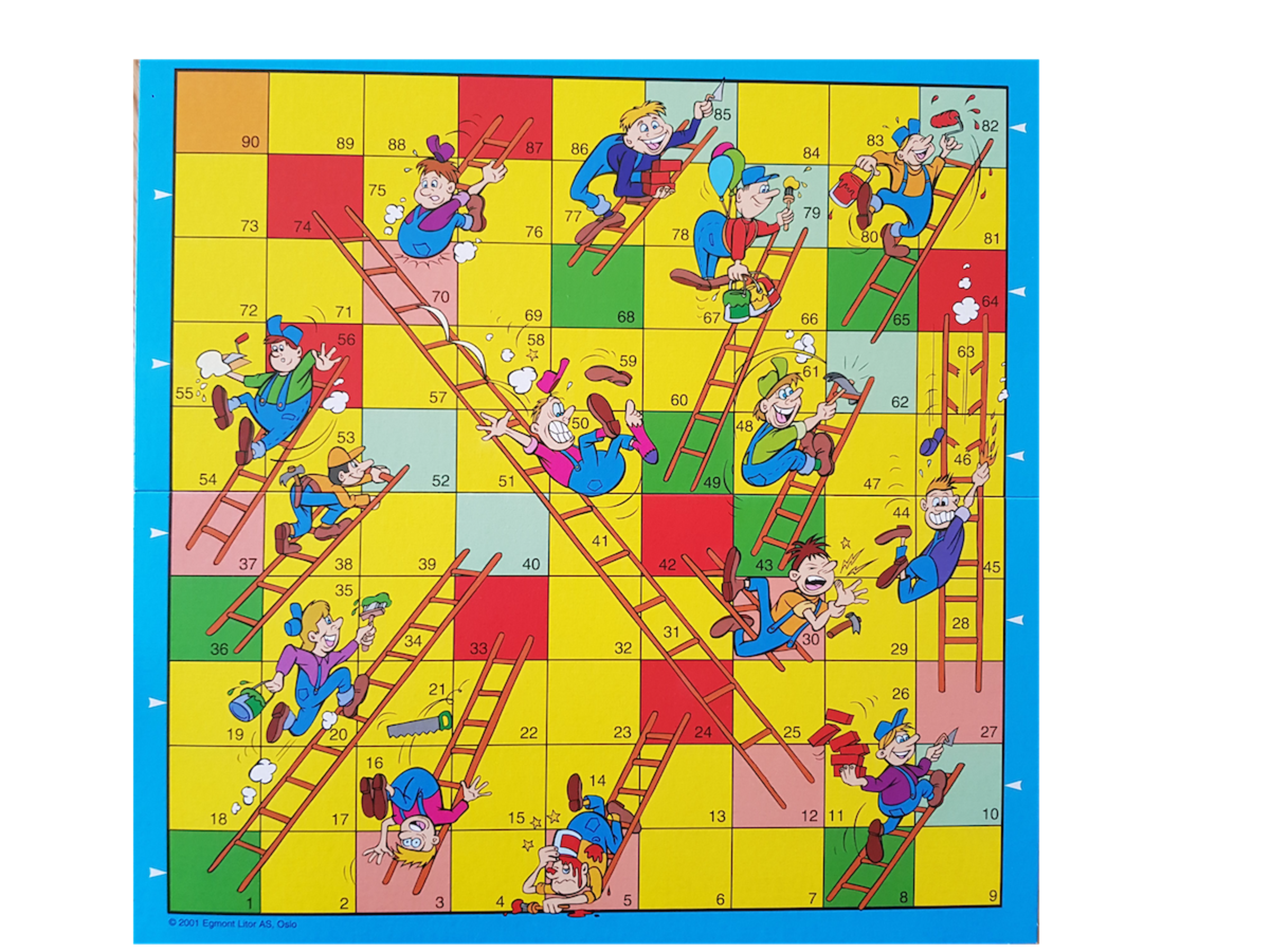
Make a python simulator for the game shown above, and run simulations to figure out the average number of throws a player need to throw in order to win. Show the distribution of the dice rolls graphically. Consider how many simulations that is necessary in order to come up with an approximate result for the average dice rolls in order to win.

Things to consider:
1: You can only win if you land on the 90th tile
2: There is only one dice
3: Start position is 0 (Tile 0)

#ComputerScience

Note by Lars André Hansen
1 year, 7 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Assuming that one can only win by landing on exactly 90, it takes about 42 rolls on average to win the game. Averaging results over 10510^5 games yields this result consistently. Even averaging over 102 10^2 games gives a "reasonably" reliable idea of the number of rolls required.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
import random

countsum = 0
numtrials = 10**5

###########################################################

for j in range(0,numtrials):

    x = 0
    rollcount = 0

    while x < 90:

        x_store = x

        roll = random.randint(1,6)

        x = x + roll

        # Ladders

        if x == 1:
            x = 40
        if x == 8:
            x = 10
        if x == 36:
            x = 52
        if x == 43:
            x = 62
        if x == 49:
            x = 79
        if x == 65:
            x = 82
        if x == 68:
            x = 85

        # Chutes

        if x == 24:
            x = 5
        if x == 33:
            x = 3
        if x == 42:
            x = 30
        if x == 56:
            x = 37
        if x == 64:
            x = 27
        if x == 74:
            x = 12
        if x == 87:
            x = 70

        rollcount = rollcount + 1

        if x > 90:
            x = x_store

    countsum = countsum + rollcount


###########################################################

avrolls = float(countsum)/float(numtrials)

print avrolls

Steven Chase - 1 year, 7 months ago
×

Problem Loading...

Note Loading...

Set Loading...