Circle Area Geometric Series

Here is a question I was asked recently (click for zoomed-in version).

Let's look at a case where the first circle has a radius of $1$ . It is a scaled version of the problem under consideration.

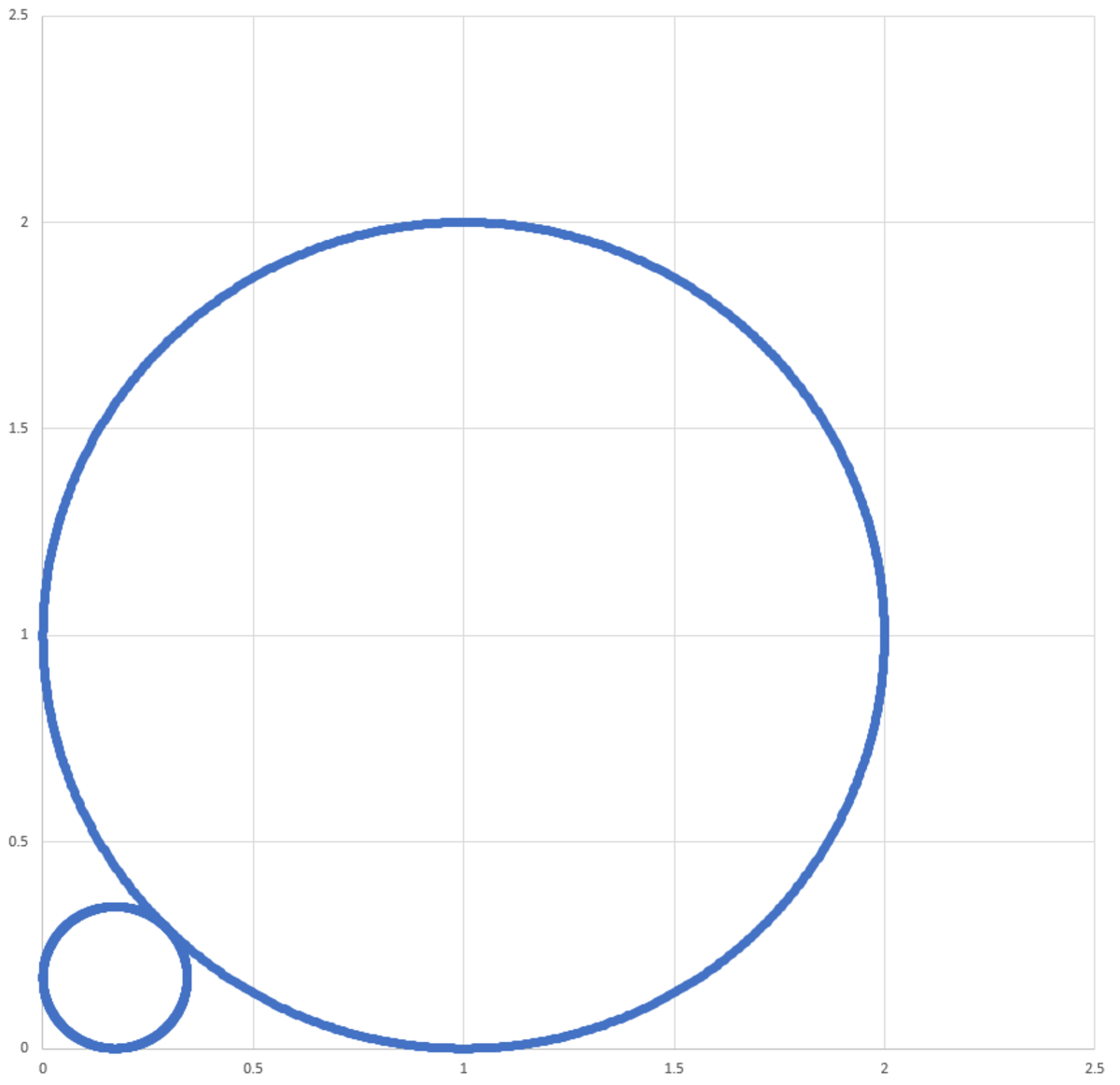
The center of the big circle is at $(1,1)$ , the center of the little circle is at $(a,a)$ , and the point of contact is $\Big(1 - \frac{1}{\sqrt{2}},1 - \frac{1}{\sqrt{2}} \Big)$ . We know that the radius of the small circle is equal to the distance from the center of the small circle to the point of contact.

$a^2 = \Big(a - 1 + \frac{1}{\sqrt{2}} \Big)^2 + \Big(a - 1 + \frac{1}{\sqrt{2}} \Big)^2$

Solving for $a$ yields $a = 3 - 2 \sqrt{2}$ . The ratio of the area of the small circle to the big circle is $a^2 = 17 - 12 \sqrt{2}$ .

Now back to the problem at hand. The area of the circle of radius $10$ is $100 \pi$ . The remaining circles follow in an infinite geometric series with common ratio $17 - 12 \sqrt{2}$ . The total area is therefore:

$A = \frac{100 \pi}{1 - (17 - 12 \sqrt{2})} = \frac{100 \pi}{12 \sqrt{2} - 16} = \frac{25 \pi}{3 \sqrt{2} - 4}$

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

@Steven Chase Thanks you so much sir.

A Former Brilliant Member - 1 year ago

@Steven Chase BTW how do you predicted that they will follow geometric progression?
Thanks in advance.

Because the small circle just becomes the new big circle, and the whole thing repeats again

Steven Chase - 1 year ago

Clever deduction. Nice!

Mahdi Raza - 1 year ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$