Circle The Ratio

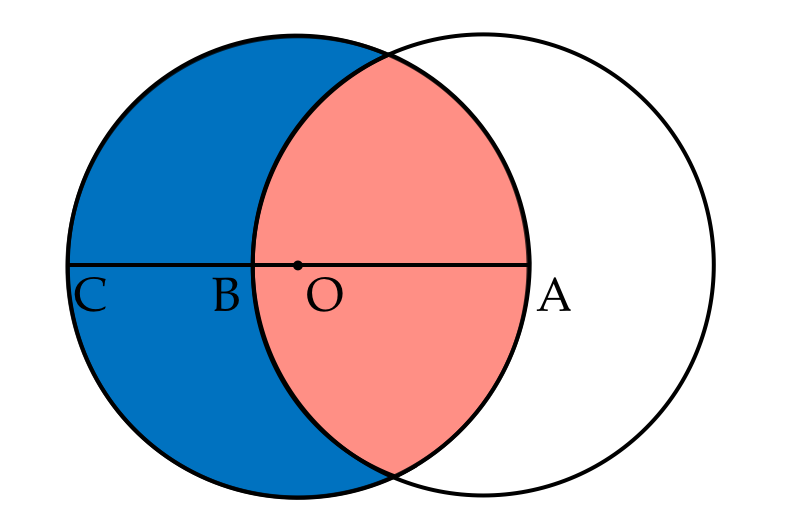
Consider 2 overlapping congruent circles, the area formed by the overlap area shown in red is equal to the remaining area shown in blue. If O is the centre of the circle, and A, O, B and C are colinear points

Then find $\frac{AB}{AC}$

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Let $D$ and $F$ be the points of intersection of the circle, let $E$ be the intersection of $AB$ and $DF$ , let $r$ be the radii of each circle, and let $\theta = \angle DOF$ .

Then the area of sector $ODAF$ is $A_{ODAF} = \frac{1}{2}r^2 \theta$ and the area of $\triangle ODF$ is $A_{\triangle ODF} = \frac{1}{2}r^2 \sin \theta$ , so the difference between them is $\frac{1}{2}r^2(\theta - \sin \theta)$ , which makes the area of the red region twice that much or $A_{\text{red}} = r^2(\theta - \sin \theta)$ . Since the red region and the blue region make a circle and the red region and the blue region are the same, the area of the red region is also the area of half the circle or $A_{\text{red}} = \frac{1}{2}\pi r^2$ . Therefore, $A_{\text{red}} = r^2(\theta - \sin \theta) = \frac{1}{2}\pi r^2$ or $2\theta - 2\sin \theta = \pi$ which solves numerically to $\theta \approx 2.3098815$ .

By trigonometry on $\triangle OED$ , $OE = r \cos \frac{1}{2}\theta$ , which means $AB = 2r - 2OE = 2r - 2r \cos \frac{1}{2}\theta$ . Since $AC = 2r$ , $\frac{AB}{AC} = \frac{2r - 2r \cos \frac{1}{2}\theta}{2r} = 1 - \cos \frac{1}{2}\theta$ . With $\theta \approx 2.3098815$ , this makes the ratio $\frac{AB}{AC} \approx \boxed{0.596027265}$ .

David Vreken - 2 years, 3 months ago

This would be a good problem for the geometry or calculus section

Steven Chase - 2 years, 3 months ago

It's very elegant indeed, and I'm surprised I never saw it before, so simple to formulate it is. But I'm not seeing any analytical or exact solution to it. The best I can get so far is an equation mixing angles and cosines, which I'm not seeing how to solve unless through numeric methods. I'll think more on it, later.

João Pedro Afonso - 2 years, 3 months ago

Hi sir how you r editing the fig which software

Uj Al Solution - 5 months, 3 weeks ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$