Circuits Problem Solution

This problem was sent to me recently. I have made some additions to the graphic.

On every time step of a numerical solution, I do the following:

1) Update the capacitor voltage based on the capacitor current from the previous time step
2) Solve for the voltage at point B based on the nodal equations at point C.
3) Solve for the capacitor current

Assume that point C is the reference voltage point, with zero voltage. Let $V_C$ denote the voltage across the capacitor. The node equation at point C is:

$\frac{0 - V_B}{R} + \frac{0 - (V_B + V_C - V)}{2 R} + \frac{0 + 2V - (V_B + V_C)}{R} = 0$

Note that $V_A = V_B + V_C - V$ . Solve the above equation for $V_B$ . Then find the current through the capacitor as follows:

$V_A = V_B + V_C - V \\ I_C = \frac{V_B - V_A}{R} + \frac{V_B - 0}{R}$

Simulation code below. Results are printed at the end of the code.

import math

# Constants

R = 1.0
C = 10.0**(-6.0)
V = 8.0

us = 10.0**(-6.0)

dt = 10.0**(-10.0)

################################

# Initialize simulation

VC = 0.0

right = (VC - V)/(2.0*R) - 2.0*V/R + VC/R
left = -2.0/R - 1.0/(2.0*R)

VB = right/left

VA = VB + VC - V

IC = (VB-VA)/R + VB/R

VCd = IC/C

################################

# Run simulation

t = 0.0

while t <= (5.0/8.0)*us:

    VC = VC + VCd*dt

    right = (VC - V)/(2.0*R) - 2.0*V/R + VC/R
    left = -2.0/R - 1.0/(2.0*R)

    VB = right/left

    VA = VB + VC - V

    IC = (VB-VA)/R + VB/R

    VCd = IC/C

    t = t + dt

################################

print dt
print t
print ""
print IC
print VA


#>>> 
#1e-08
#6.3e-07

#5.79176835692
#2.55205791077
#>>> ================================ RESTART ================================
#>>> 
#1e-09
#6.25e-07

#5.88135906014
#2.52966023496
#>>> ================================ RESTART ================================
#>>> 
#1e-10
#6.25e-07

#5.88560014166
#2.52859996458
#>>>

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

@Steven Chase Thanks for the solution.

A Former Brilliant Member - 11 months ago

@Steven Chase can we solve this using pen and page only??

I would like to see the official solution. The numerical solution seems much more natural to me, as usual. I also think it is interesting that they are asking for approximations.

Steven Chase - 11 months ago

@Steven Chase the official solution is not available in website , in that image you can see it is written NA which means not available.
I will say my physics teacher to upload the solutions now.

@A Former Brilliant Member – Is this your schoolwork or a problem from a university textbook?

Krishna Karthik - 11 months ago

@A Former Brilliant Member – If this is your schoolwork, I must say your school is quite hard.

@Krishna Karthik – @Krishna Karthik this is work of a problem like of JEE.
But it is not in our school course .
I have separately joined a Institute (coaching) for JEE preparation.

@A Former Brilliant Member – Ah. that explains it. Holy shit... JEE's hard. Lol I live in Australia so I can't try JEE. I'm doing IB physics Higher Level; it's sort of in-between JEE and AP Physics.

Bro, you'll definitely get into IIT though. You're already way ahead lol

@Krishna Karthik – @Krishna Karthik i can give jee advance papers. Do you want to try those problems.??
I have jee level millions of problems.

@A Former Brilliant Member – Sure! Thank you so much bro. But only classical mechanics. I haven't started on Electromagnetism yet lol

@Krishna Karthik – @Krishna Karthik no problem. I have separate practice problem for each topic. . But the condition is you have to use ony Pen and page.

@A Former Brilliant Member – Yes; of course. I'll try my best. Beautiful!

@A Former Brilliant Member – It'll be amazing practice for my physics exams.

@A Former Brilliant Member – Did you try my new problem btw? I have to see if my solution's right...

@Krishna Karthik – @Krishna Karthik did you have studied Thermodynamics??

@A Former Brilliant Member – No, not yet. I am working mostly on my maths and computer science; physics is kind of my side thing that I teach myself on brilliant.

This is because I haven't formally started physics in school yet.

I have started on Special Relativity though lol. It's easier than thermodynamics for sure, but I might start on it soon.

@Krishna Karthik – @Krishna Karthik so basically you want mechanics. I am giving you 27 problems.
2-3 are not in mechanics you can neglect them .

@A Former Brilliant Member – Thanks! Epic bro.

@Krishna Karthik – @Krishna Karthik Brilliant is not accepting PDF. Let me you 4-5 photos.

@A Former Brilliant Member – You can upload the photos onto a discussion. Photos are fine. Thx mate!

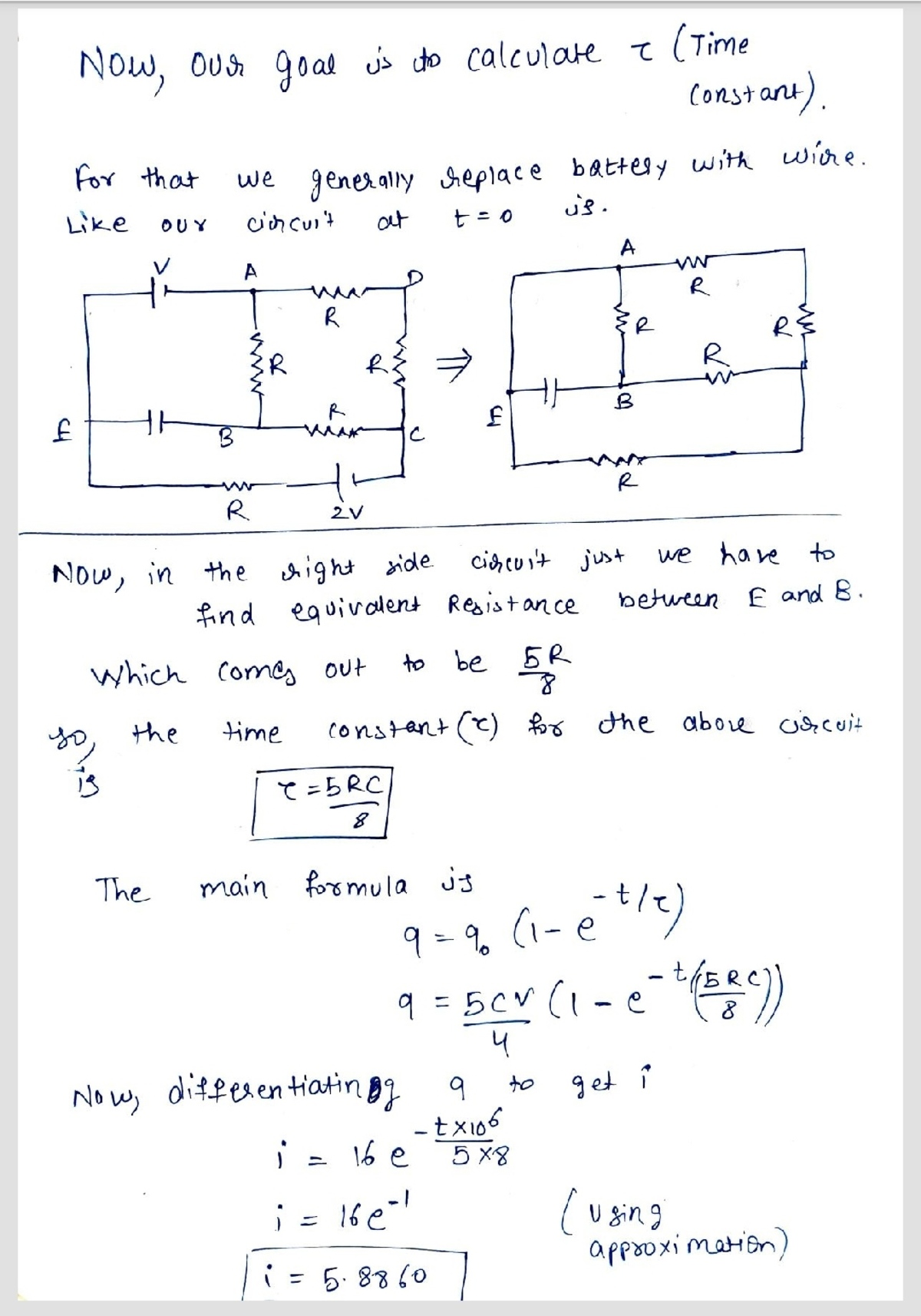
@Steven Chase sir the hand made solution is ready.
In the first page (in our school, we have been taught that you don't have to derive left in every question)
But for explaining I have derived for you.
My friends always follow school teachers and use this method and I always solve differential equation for this problems .
What do you think which method is best ?
BTW the official solution are not yet uploaded in the website, I solved 1st problem myself and here is the solution below.

Generally speaking, differential equations and ground-up mathematics is the correct way to do physics. But for high-school or on a test it'll take time to derive, so I just use formulas for high-school.

And literally all laws in physics are written in the form of ODEs and PDEs, so high-school just uses approximations or makes some values constant so that rates of change and calculus doesn't have to be used. For obvious reasons as not everyone is a maths wiz.

@Steven Chase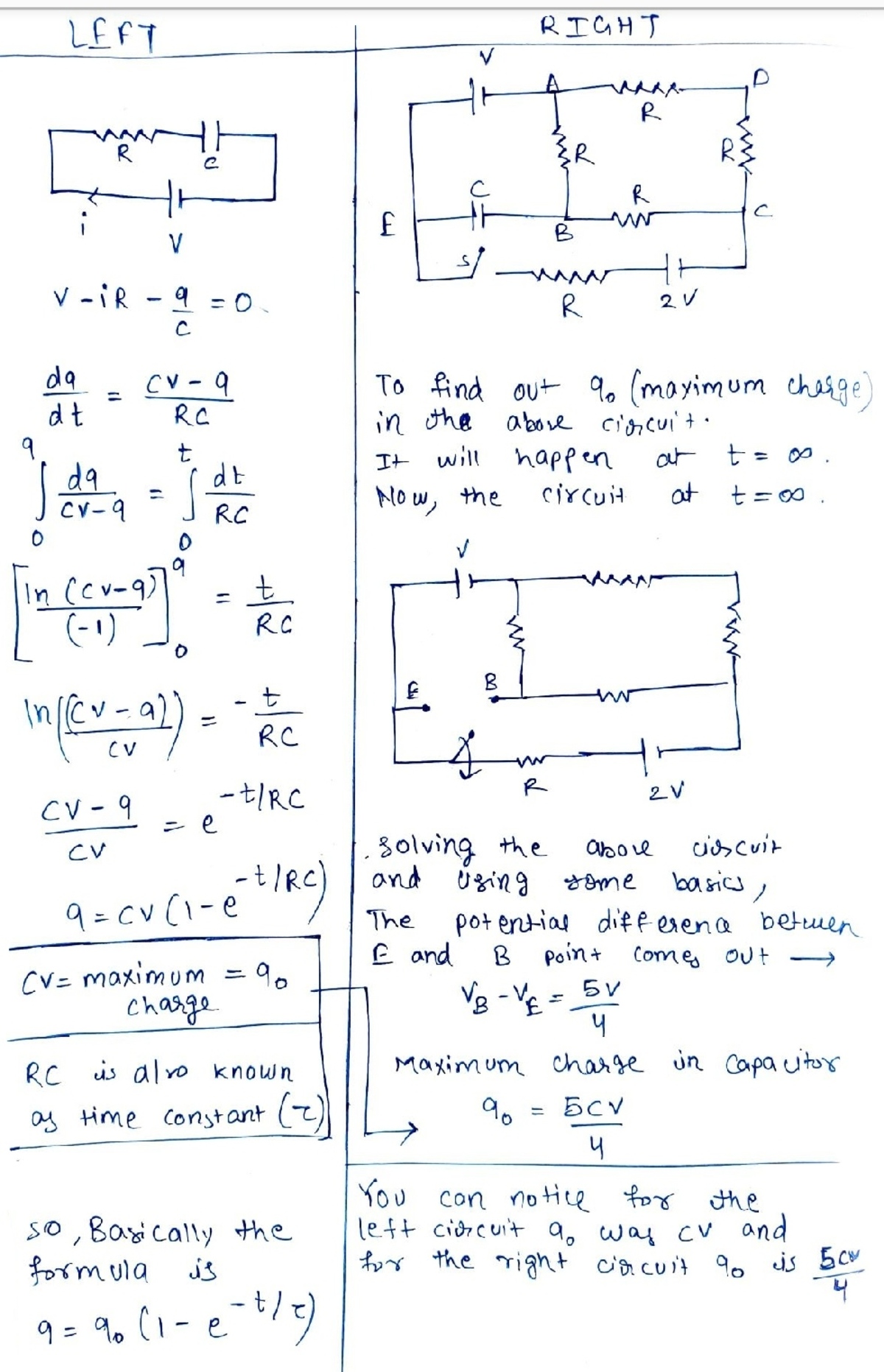

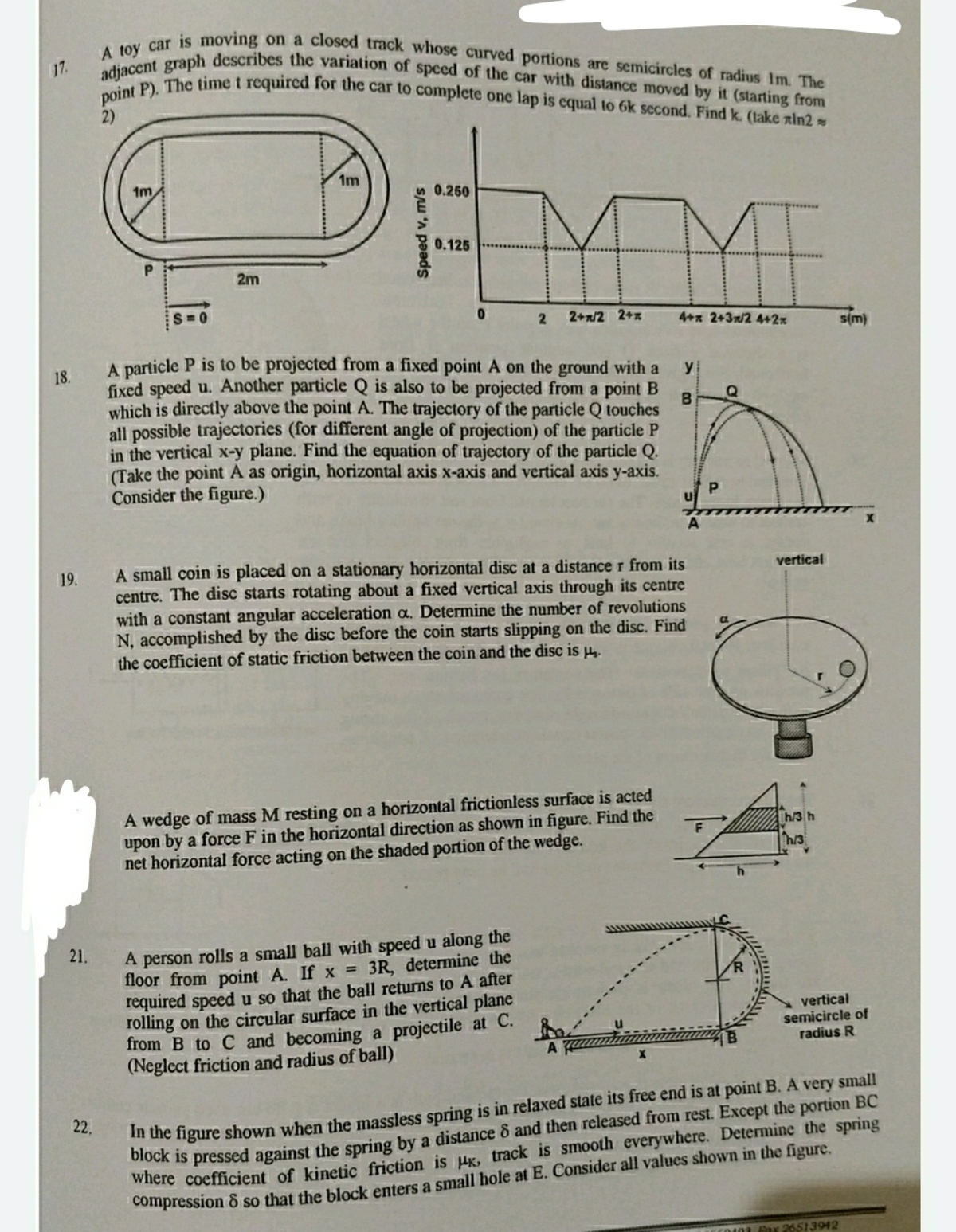
@Steven Chase sir did you have seen this type of method.

That's kind of a nice approach. It just depends on what tools you're allowed to use

By the way, I'm planning to make a time-domain version of your maximum power transfer problem, if that's OK with you

@Steven Chase did you have woke up now??

@Steven Chase why not sir? It will be interesting.

@Krishna Karthik

Thx! Cheers

@Krishna Karthik you can print it out. It will be helpful.

@Steven Chase is it uploaded now??

Yes, it is

Hmmm... I wonder... Why has Neeraj Anand Badhgujar deleted his account?

@Krishna Karthik – There was a bit of drama earlier that I won't describe in detail. I don't think he needed to delete his account though.

@Steven Chase – What happened though? He was a friend. I hope you won't mind telling me... it's alright if you won't though... thanks

@Steven Chase I am getting these 2 equations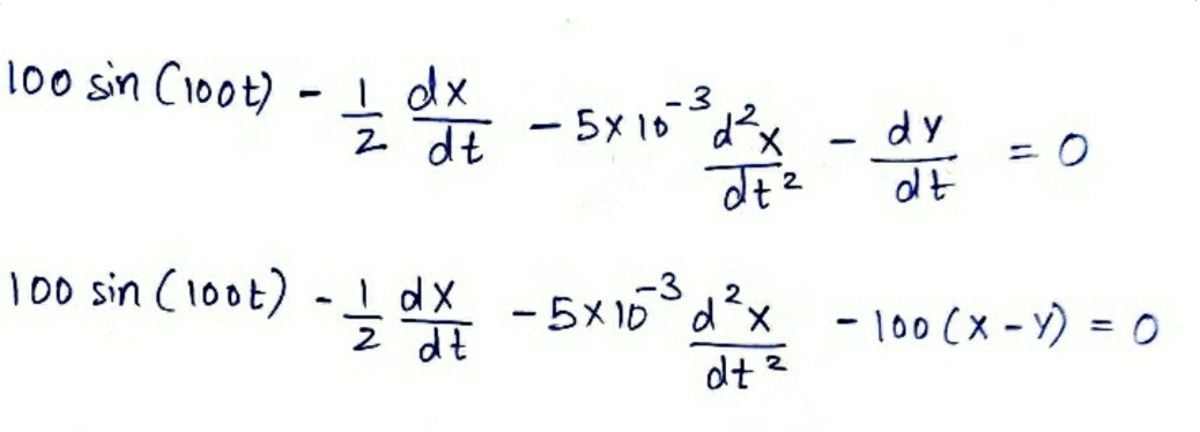
x and y are charges And Wolfram has failed to solve and I don't think I can solve this with laplace.
So I am planning to use python
But I didn't know how to use python for this work. Can you please little bit guide me?

On every time step, you can do:

x = x + xd*dt 
y = y + yd*dt 
xd = xd + xdd*dt 
yd = yd + ydd*dt 
xdd = (insert expression here) 
ydd = (insert expression here)

That is just a general format. You can modify as necessary

Thanks, but how to solve this differential equations??

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$