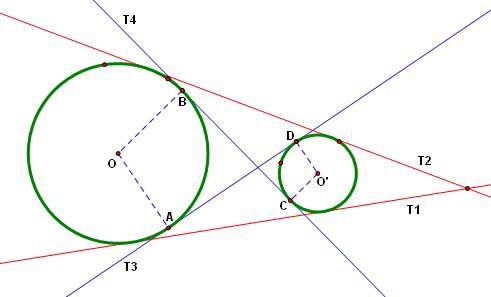
Common tangent rules

Problem 29 on the JEE mains inspired this note:

Things to know

•Pythagorean theorem

•Graphical transformations (only vertical and horizontal shifts)

This note will describe a quick and easy way to find the number of common tangents to two circles.

Given the following equations for the circles:

(y−a)2+(x−b)2=r2 (y-a)^2+(x-b)^2=r^2

y2+x2=s2y^2+x^2=s^2

find the number of common tangents these circles will have.

You may wonder, "this isn't generalized, you assume one is at the origin". Let me explain.

What I did was move both circles pp units along the x-axis and qq units along the y-axis to make one at the origin. The number of tangents to the circles won't change if we perform a transformation other than a distortion.

Now for the tangent rules: how many common tangents will they have if...

I) a2+b2=(r+s)2a^2+b^2=(r+s)^2 then there are 3 common tangents.

II) a2+b2>(r+s)2a^2+b^2>(r+s)^2 then there are 4 common tangents.

Now for case 3

III) a2+b2<(r+s)2a^2+b^2<(r+s)^2 then we have three cases

NOTE: you must check this first, don't immediately check the rules below (Quick rule, if r=s in this case, then there are 2 tangents).

III-1) a2+b2=(r−s)2a^2+b^2=(r-s)^2 then there is 1 common tangent.

III-2) a2+b2>(r−s)2a^2+b^2>(r-s)^2 then there are 2 common tangents.

III-3) a2+b2<(r−s)2a^2+b^2<(r-s)^2 then there are no common tangents.

#Algebra #Geometry #Tangent #AnalyticalGeometry #Easymoney

Note by Trevor Arashiro
6 years, 2 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

Can you tell me such way in finding common tangents to a circle &a ellipse ?

Anubhav Bhatia - 6 years, 2 months ago
×

Problem Loading...

Note Loading...

Set Loading...