Complex motion part 2

1.A solid cone of length $h$ and half angle $\alpha$ is rolling on a plane about its vortex with an angular velocity of $\Omega\hat{k}$ , as shown in Fig. Compute the angular velocity, angular momentum, and kinetic energy of the cone. 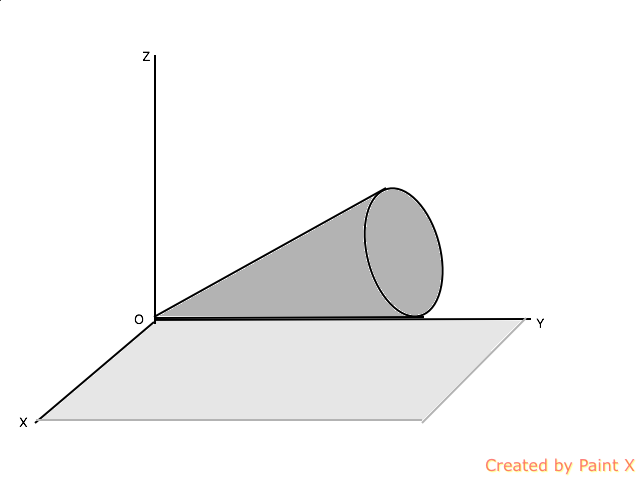2. 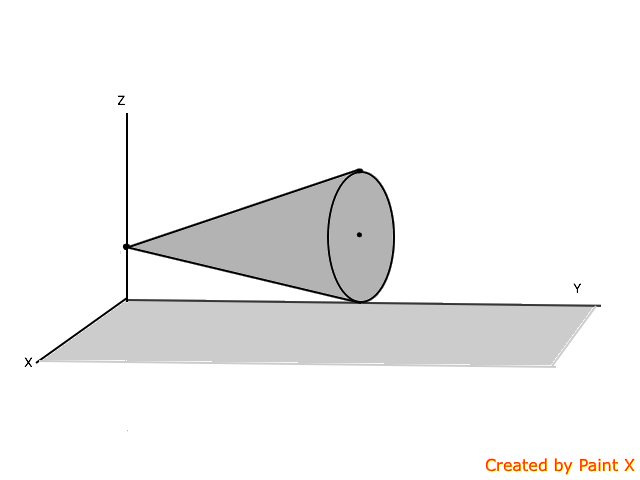The vertex of the aforementioned cone is fixed on the $z$ axis at a height equal to the radius of the cone. The cone rotates an angular velocity of $\Omega\hat{k}$ about the vertical axis as shown in Fig. Compute the angular velocity, angular momentum, and kinetic energy of the cone.

#Mechanics

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Here is my attempt at the second one. There are two rotations to consider:

1) The rotation of the cone about its own axis
2) The rotation of the cone about the vertical axis

Let $H$ be the height of the cone, $R$ be the radius of the cone, and $\alpha$ be the semi-angle.

$tan \, \alpha = \frac{R}{H} \\ H = \frac{R}{tan \, \alpha}$

Let the angular speed of the cone with respect to the vertical axis be $\omega$ , and the angular speed of the cone with respect to its own axis be $\omega'$ . They are related as follows (assuming no slipping):

$H \, \omega = R \, \omega'$

Let $I$ and $I'$ be the moments of inertia with respect to the vertical axis and the cone axis, respectively.

$I = \frac{3}{20} \, M \, (R^2 + 4 H^2) \\ I' = \frac{3}{10} \, M \, R^2$

The kinetic energy is then (angular momentum is similar):

$E = \frac{1}{2} I \, \omega^2 + \frac{1}{2} I' \, \omega'^2 \\ \frac{3}{40} \, M \, (R^2 + 4 H^2) \, \omega^2 + \frac{3}{20} \, M \, R^2 \, \omega'^2 \\ = \frac{3}{40} \, M \, R^2 \, \Big( 1 + \frac{4}{tan^2 \, \alpha} \Big) \, \omega^2 + \frac{3}{20} \, M \, R^2 \, \frac{1}{tan^2 \, \alpha} \, \omega^2 \\ = \frac{3}{40} \, M \, R^2 \, \omega^2 + \frac{9}{20} \, M \, R^2 \, \frac{1}{tan^2 \, \alpha} \, \omega^2$

Steven Chase - 2 years, 3 months ago

Thx @Steven Chase sir got.it.(How to.solve first one any ideas ? As such axis of rotation would.be at an angle.from angular.momentum vector right )??

Kudo Shinichi - 2 years, 3 months ago

I'll start thinking about the first one. Did I get the second one right?

Steven Chase - 2 years, 3 months ago

@Steven Chase – Yes u r right @Steven Chase Sir ( David morin has the first part of the problem in it , but I dont know how they approach the question) . ( they confused me by adding angular momentums )

Kudo Shinichi - 2 years, 3 months ago

@Kudo Shinichi – Can you post the energy expression for the first part, so I can check my answer when I have it?

Steven Chase - 2 years, 2 months ago

@Steven Chase sir pls share how ur way of solving these 2 problem ? @Aaghaz Mahajan bro pls help u also ?

Kudo Shinichi - 2 years, 3 months ago

Do you know the answers? I think the second one should be fairly easy. The first one will take a bit more work.

Steven Chase - 2 years, 3 months ago

@Steven Chase sir, Can u solve for second part and later first part sir? (Yes I know answers for second part .)

Kudo Shinichi - 2 years, 3 months ago

@Kudo Shinichi – Ok, I'll do the second part for now

Steven Chase - 2 years, 3 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$