Complex Networks 8

(It is assumed that reader has already read Seventh article of this series)

(Follow me on twitter at @ShekatkarSnehal)

In the last article we talked about Watts-Strogatz model and the way in which it tries to explain two observed properties of the real world networks: small world property and high clustering. Before we move forward, we now need to make a big qualitative change to the picture of network that we are talking about so far. The networks that we saw so far are undirected: edges in these networks do not have direction. But not all networks are like that. For example consider our favorite social network. In this network, it is not always true that if a certain person knows another person, then that other person must know this person as well. Usually we know many famous people like movie actors, politicians, players and so on who do not know us. Thus the edges that join you to such people should really speaking be directed. We represent such directed network using arrow at the end of edge. If there is two way interaction, then we would have arrow at both the ends of that particular edge. Following diagram shows a typical directed network.

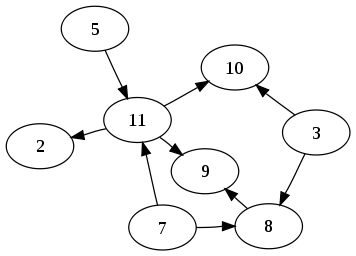
Before moving ahead let us try to find few more examples of directed networks around us. As I have already mentioned that world wide web (www) is a network of web-pages connected by hyper-links. But we are very well aware that most of the time we can go from one page to other but not back. For example, my homepage has link to Google but Google doesn't have hyper-link to my page! Thus www is a directed network. Similarly the citation network of scientific articles, in which articles are nodes and citations are links is a directed network. The network of neurons in brains (if gap junction type of couplings are ignored) is again a directed network. Networks representing various ecosystems are directed network because most of the time, predator-prey relationship is one way (Fortunately fishes do not capture and eat humans even though human do capture fishes!). You might want to amuse yourself by trying to find more examples of directed networks around you (Post them in the comments if you find one!).

What about adjacency matrix of directed network? It's easy to see that this matrix is in general asymmetric unlike symmetric for undirected networks. This makes the mathematical analysis for directed networks somewhat complicated and hence whenever possible, we will try to avoid it. But few things are worth noting. There are two types of degrees for every node in directed network: in-degree and out-degree. n-degree of a node is defined as the number of edges that point to the given node and out-degree of node is defined as the number of edges that point out from the given node. This also means that there are two types of distributions for directed networks : $p_{in}(k)$ and $p_{out}(k)$. The form of these two distributions for real world networks is quite surprising for some real world networks. We will look into these issues in upcoming articles.

Keep giving feedback!