Complex Numbers Help needed.

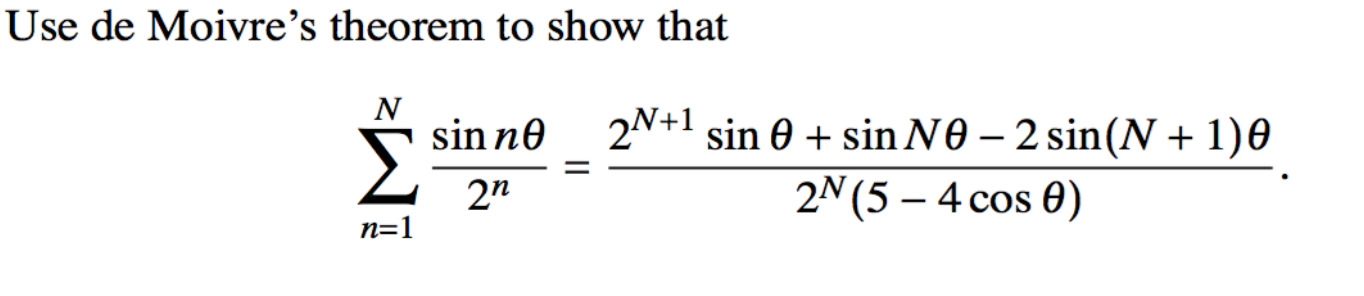
I tried the following approach.

Let \( z = \dfrac{ e^{ i \theta }}{2} \). Then using de Moivre's theorem:

$\sum _ { n = 1 } ^ { N } \frac{ \sin n \theta } { 2 ^ n } = \text { Im } \left ( \sum _ { n = 1 } ^ { N } z^ { n} \right)$

This is sum of GP. Using the sum of GP:

$\sum _{ n = 1 } ^{ N } z^ { n} = \frac{ \frac{e ^{ i \theta } } { 2 } ( 1 - \frac{e ^{ N i \theta } } {2^ { N } } ) } { 1- \frac{ e^{i \theta } } { 2 } }$

This simplifies to:

$\sum _{ n = 1 } ^{ N } z^ { n} = \frac{ e ^{ i \theta } ( 2 ^ { N } - e ^{ N i \theta } ) } { 2 ^ { N} ( 2- e^{i \theta } ) }$

$\sum _{ n = 1 } ^{ N } z^ { n} = \frac{ ( 2 ^ { N } e ^{ i \theta } - e ^{ (N + 1 ) i \theta } ) } { 2 ^ { N} ( 2- e^{i \theta } ) } ~~~~~ (*)$

Now I changed the complex numbers on the RHS from Euler's form to cis form, then made the denominator real and finally took imaginary part of the expression. Is there a simpler way to solve this problem? My method is very complicated, thus error-prone.

In fact, I have already made an error which is why I have posted this note. I am getting the RHS as

$\frac{2 ^ { N + 1 } \sin \theta - 2 \sin (N + 1) \theta } {2 ^ N (5 - 4 \cos \theta) }$

i.e. without the $\sin N \theta$ term in the numerator. Where is the $\sin N \theta$ term coming from? There are only $e^{ i \theta }$ and $e ^{ (N + 1 ) i \theta }$ in the $(*)$ equation. I can't seem to find out where I have gone wrong.

Please help.

Thanks.

Source: CIE A Levels Further Maths May / June 2007 Q 11 (b)