ComplexBash: A touch of vectors

This note is related to the previous note, please have a look if you haven't read that one.

This note deals with \(\color{Brown}{\text{the basics of complex numbers}}\) and \(\color{Purple}{\text{some useful results}}\) that will be needed in bash solutions.

Also, 2 examples of ComplexBash solutions, which might surprise you by their shortness over Pure geometry solutions.

The name of the note is $\color{#20A900}{\text{Touch of vectors}}$ , because complex numbers can be treated like vectors and that makes things easier at times. In fact, solutions that use vectors are many times very similar, except for the calculations.

$\huge{\circledast}$ Before that, I want to discuss some things about how they mark the bash solutions in Olympiads (at least in India). Take these as your rules for bashing:-

$\mathbf{1.}$ If you are stumped in a problem and are finding no way to get a solution by pure geometry, then only use bash.

$\mathbf{2.}$ If you are getting a strong feeling that the problem is not easy by pure geometry and you’ll not get going with pure geometry, start bashing.

$\mathbf{3.}$ Once you’ve started a bash solution, COMPLETE IT! Because in the marking scheme, they have one thing in mind, a bash solution is either a full mark solution or a 0.

$\mathbf{4.}$ When you are bashing, do not leave loose ends, like “The above equation reduces to zero after calculation, hence…” $\color{#D61F06}{\text{NO!!}}$

You have to actually do ALL the calculations that are necessary and show the result, not just state it.

$\color{#3D99F6}{\text{The very basics of Complex Numbers}}$ (skip if you know already)

$\boxed{\Large{ i= \sqrt{-1}}}$

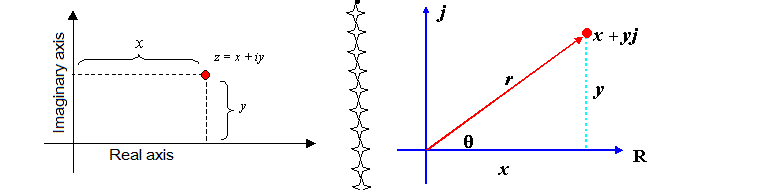
• Every complex number $z$ will have a magnitude $|z|$ and an angle that it makes with the real axis, called it’s argument , denoted by $arg(z)$ and always $-\pi < arg(z) \leq \pi$ This is why we can treat complex numbers as vectors whenever required.

• If $z=x+iy$, then $|z|=\sqrt{x^2+y^2}$ and $arg(z) = tan^{-1}\frac{y}{x}$.

• A complex number of unit modulus making an angle $\theta$ with real axis will be given by $e^{i\theta}=\cos\theta+i\sin\theta \implies z = |z| e^{i\theta}$

• Argument of all positive real numbers is $0$ and that of all negative real numbers is $\pi$

$\quad\quad$ Argument of all numbers of the form $ki$ is $\frac{\pi}{2}$ for $k>0$ and $\frac{-\pi}{2}$ for $k<0$.

• Every complex number is equivalent to a vector from Origin (complex number 0) to the point where it is denoted. Thus $z= (z-0)$, a vector segment from $0$ to $z$.

• The complex number equivalent to the vector segment between $A$ and $B$ will be $\vec{AB}=b-a$ , and $\vec{BA}=a-b$.

• $arg(z_1z_2)=arg(z_1)+arg(z_2)$, adjust the $2\pi$ addition/subtraction to bring it in the range($-\pi,\pi$]

• $\dfrac{z_1}{z_2} = \dfrac{|z_1|}{|z_2|} \times e^{i\theta}$ , where $\theta$ is the angle to be traced from $z_2$ in anticlockwise direction, in order to reach the direction same as $z_1$. Thus in other words, $\theta = arg(z_1)-arg(z_2)$.

• As in above thing $|z_1|,|z_2|$ will be some real values, we can say $z_1 = k\times z_2 \times e^{i\theta}$ for all $z_1,z_2$ with $z_2\neq 0$.

$\quad\quad$ (Yeah, division by zero is not allowed in complex numbers too!)

$\quad\quad$ $k$ will be a real number which will help us adjust the magnitude of our complex number.

With this much machinery, we are equipped enough to obtain some results we’ll be actually needing in geometry problems, so let’s begin the actual bashing!

The notations will be standard, (G,H,O etc) except for $a,b,c$, which won’t be sides of triangles but the complex coordinates of the vertices $A,B,C$ respectively.

Here are $\color{#3D99F6}{\text{Some Results}}$ that will prove helpful,

(not dealing with their proofs, we want the ‘Use’ of them more than ‘Proof’)

$\boxed{1}$. Midpoint of segment between $z_1,z_2$ will be $\dfrac{z_1+z_2}{2}$

$\boxed{2}$. Centroid of a triangle with vertices $z_1,z_2,z_3$ will be $\dfrac{z_1+z_2+z_3}{3}$.

$\boxed{3}$. In a $\triangle ABC$, points $O,G,H$ are circumcenter, centroid, orthocenter respectively.
$\quad\quad$ As we know by Euler line, $2\vec{OG}=\vec{GH}$. If we take the complex numbers assigned to $O,G,H$ as $o,g,h$, then $2(g-o)=(h-g)$

$\therefore 2\left( \dfrac{a+b+c}{3} -o\right) = \left( h- \dfrac{a+b+c}{3} \right)$

$\quad\quad$ Now if we take the circumcircle of $\triangle ABC$ to be centered at origin, we get $2g=h-g \implies h=a+b+c$

In general, $h=a+b+c - 2o$, where $o$ is circumcenter coordinates.

$\boxed{4}$. If $\triangle ABC$ is equilateral, we have $|a-b|=|b-c|=|c-a|$ .

Also, if the names of vertices $A,B,C$ are in anticlockwise order, then $\vec{BA}$ is obtained by rotating $\vec{BC}$ by $60^\circ$ in anticlockwise direction,

$\therefore (a-b)=(c-b)e^{i\frac{\pi}{3}}$

$\boxed{5}$. If $AB \bot CD$, then you can say $(b-a)=k(c-d) i$ , where $k=\frac{|b-a|}{|c-d|}$ ,

Because $e^{i\frac{\pi}{2}}=\cos\frac{\pi}{2}+i\sin\frac{\pi}{2} = i$.

Now something interesting,

$\color{#3D99F6}{\text{Problems that use what’s discussed till now !}}$

Problems in this note are bit basic, but I feel you might feel them cool as the complex bashes are shorter than pure geometry... from next one there will be problems from Olympiads !

$\boxed{\mathbf{1}}$ Given any $\triangle ABC$, equilateral triangles are constructed externally on the sides of the triangle, to obtain points $P,Q,R$. Prove that centroid pf $\triangle PQR$ is same as centroid of $\triangle ABC$.

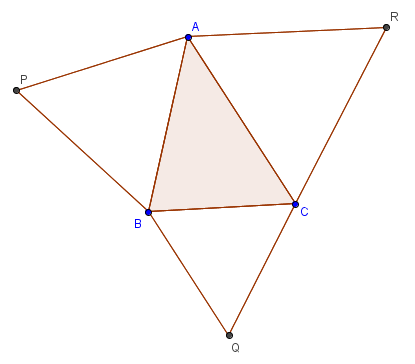
$\textbf{Bash}$ – Let original triangle have complex coordinates $a,b,c$.

Now let’s use the simple fact that $PB$ is obtained by rotating $BA$ by $60^\circ=\frac{\pi}{3}$.

$\therefore (p-b)=(a-b)e^{i\frac{\pi}{3}} = (a-b)\left(\frac{1+\sqrt{3}i}{2}\right)$

$\therefore p=\frac{a+b}{2} + \frac{(a-b)\sqrt{3}i}{2}$

Similarly, $q= \frac{b+c}{2}+\frac{(b-c)\sqrt{3}i}{2}$ ; $r=\frac{c+a}{2}+\frac{(c-a)\sqrt{3}i}{2}$

Now centroid of $\triangle PQR = \frac{p+q+r}{3} = \dfrac{\frac{a+b}{2}+\frac{b+c}{2}+\frac{c+a}{2}+\frac{(a-b)\sqrt{3}i}{2}+\frac{(b-c)\sqrt{3}i}{2}+\frac{(c-a)\sqrt{3}i}{2}}{3} = \dfrac{a+b+c}{3}$

As centroid of $\triangle ABC$ is also $\dfrac{a+b+c}{3}$, we have proved the required result.

$\color{#D61F06}{\textbf{Note :-}}$ This will have solutions by pure geometry, but you can see they need more brain and are longer than what we did above….. But what’s more noteworthy is, imagine doing this by coordinate bash… You’d sink in the calculations to get points P,Q,R only!

$\boxed{\mathbf{2}}$ On the sides of $\triangle ABC$, squares are constructed externally ($\Box ABQP, \Box BCSR , \Box CAUT$). Prove that centroids of triangles $\triangle ABC , \triangle PRT , \triangle QSU$ are all the same point.

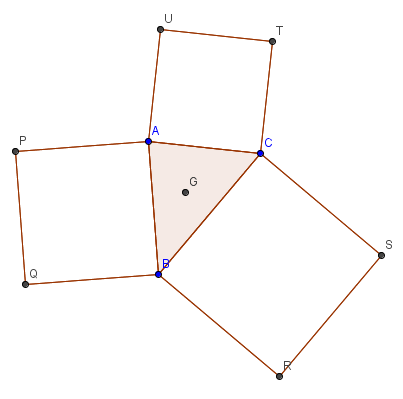
$\textbf{Bash}$ – We use that $AP$ is rotated by $90^\circ = \frac{\pi}{2}$ in anticlockwise direction in order to get $AB$.

$\therefore (p-a) \times e^{i\frac{\pi}{2}} = (b-a) \\ \therefore (p-a)i = (b-a) \\ \therefore (p-a) i^2=(b-a)i\\ \therefore -p+a=(b-a)i \\ \therefore p=a+(a-b)i$

Now observe that $Q$ is just shift of $P$ by complex number $\vec{AB}=(b-a)$

$\therefore q=p+(b-a)=b+(a-b)i$

Similarly, we get all the required points, which are

$p=a+(a-b)i \\ q=b+(a-b)i \\ r=b+(b-c)i \\ s=c+(b-c)i \\ t= c+(c-a)i \\ u=a+(c-a)i$

Now it’s just easy calculation to find,

centroid of $\triangle PRT = \dfrac{ a+(a-b)i + b+(b-c)i + c+(c-a)i }{3}=\dfrac{a+b+c}{3}$

centroid of $\triangle QSU=\dfrac{ b+(a-b)i + c+(b-c)i + a+(c-a)i }{3} =\dfrac{a+b+c}{3}$

$\color{#D61F06}{\textbf{Note:-}}$ It’s noteworthy again that this solution is shorter and less brainy than Pure geometry and also, uses really very less calculations than Coordinate geometry…

With this, I’m concluding this part 2.

From next note onwards, there’ll be useful results and problems from past Olympiads.

If you enjoyed this, please share with your friends, who might be interested and seek help.

Stay tuned for more fun,

Happy Problem solving!