Conversion of Differential Equation to Difference Equation - Zero Order Hold

Off late I have been posting a lot of problems based on the general dynamic system of the form:

$\dot{x} = x + u$

Here, $x=x(t)$ represents a time-dependent quantity of the system whereas $u = u(t)$ is a time-varying input meant to excite the system. The behaviour of this system is captured using the differential equation described above. This note describes how to convert a differential equation to a discrete-time difference equation.

Consider the differential equation:

$\dot{x} - x = u$ Multiplying both sides by $e^{-t}$ gives: $e^{-t}\dot{x} - e^{-t}x = e^{-t}u$

This can be simplified to:

$\frac{d}{dt}\left(e^{-t}x\right) = e^{-t}u$

Or:

$d\left(e^{-t}x\right) = ue^{-t} dt$

Given that the initial condition of the system is $x(0) = x_o$, integrating both sides:

$\int_{x_o}^{xe^{-t}} d\left(e^{-t}x\right) = \int_{0}^{t} u(s)e^{-s} ds$

Which is:

$xe^{-t} - x_o = \int_{0}^{t} u(s)e^{-s} ds$

Implies:

$x(t) = x_oe^{t} + e^{t}\int_{0}^{t} u(s)e^{-s} ds$

Consider a general time $t_1 = T$ and another time instant $t_2 = T + h$, where $h$ represents a small time step.

$x(T) = x_oe^{T} + e^{T}\int_{0}^{T} u(s)e^{-s} ds$ $x(T+h) = x_oe^{(T+h)} + e^{(T+h)}\int_{0}^{T+h} u(s)e^{-s} ds$

Which can be written as: $x(T+h) = x_oe^{(T+h)} + e^{(T+h)}\int_{0}^{T} u(s)e^{-s} ds + e^{(T+h)}\int_{T}^{T+h} u(s)e^{-s} ds$

Or, $x(T+h) = e^h\left(x_oe^{(T)} + e^{(T)}\int_{0}^{T} u(s)e^{-s} ds\right) + e^{(T+h)}\int_{T}^{T+h} u(s)e^{-s} ds$

Recognising that the term in the bracket multiplied by $e^h$ is $x(T)$ gives:

$x(T+h) = e^hx(T) + \int_{T}^{T+h} u(s)e^{(T+h-s)} ds$

Addressing the remaining integral: Taking $T+h-s = z$, plugging into the integral, manipulating and simplifying gives:

$x(T+h) = e^hx(T) + \int_{0}^{h} u(T+h-z)e^z dz$

The only assumption made in this entire analysis is that $x(T)$ and $u(T)$ are held constant in the interval $[T,T+h)$ . In other words, $u(T+h-z) = u(T)$ as $z$ varies from $0$ to $h$. This leads to:

$x(T+h) = e^hx(T) + \left(\int_{0}^{h} e^z dz\right) u(T)$

In other words:

$x(T+h) = a x(T) + b u(T)$

Where: $a = e^h$ and $b = \int_{0}^{h} e^z dz$

So, in summary, this analysis shows the conversion of a differential equation to a discrete-time difference equation.

$\dot{x} = x + u$

Is equivalent to, in discrete time:

$\boxed{x(T+h) = a x(T) + b u(T)}$

Where: $\boxed{a = e^h}$ and $\boxed{b = \int_{0}^{h} e^z dz}$

Now, an example is presented to illustrate this process:

Consider the equation:

$\dot{x} = x + u$

Here, $x(0) = 0$ and $u(t) = 1$ is a constant input. This differential equation is converted to a discrete difference equation and both systems are simulated. The plots show the response of this system for various time steps $h$. In the first plot, $h = 0.1$ s. In the second plot, $h = 0.05$ s. In the third plot, $h = 0.01$ s. In the fourth plot, $h = 0.001$ s.

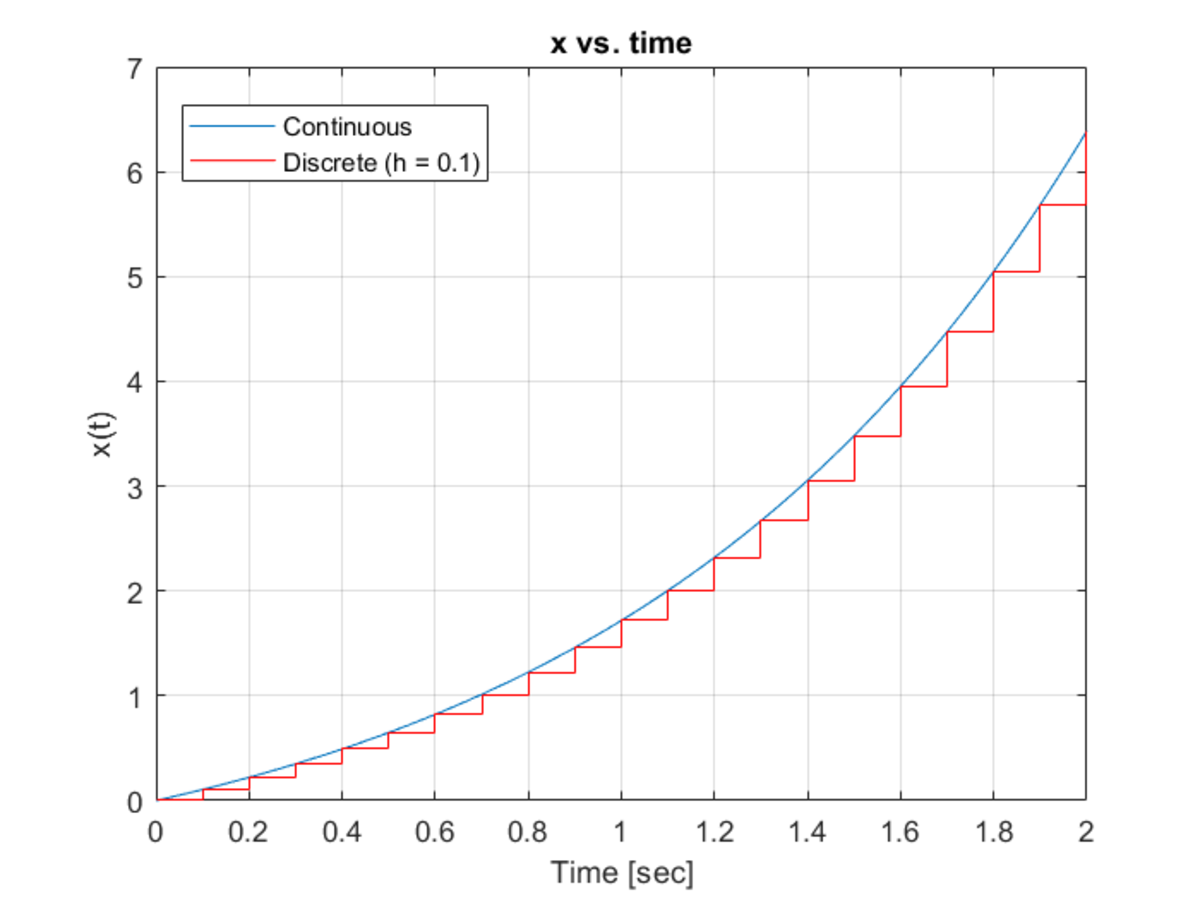
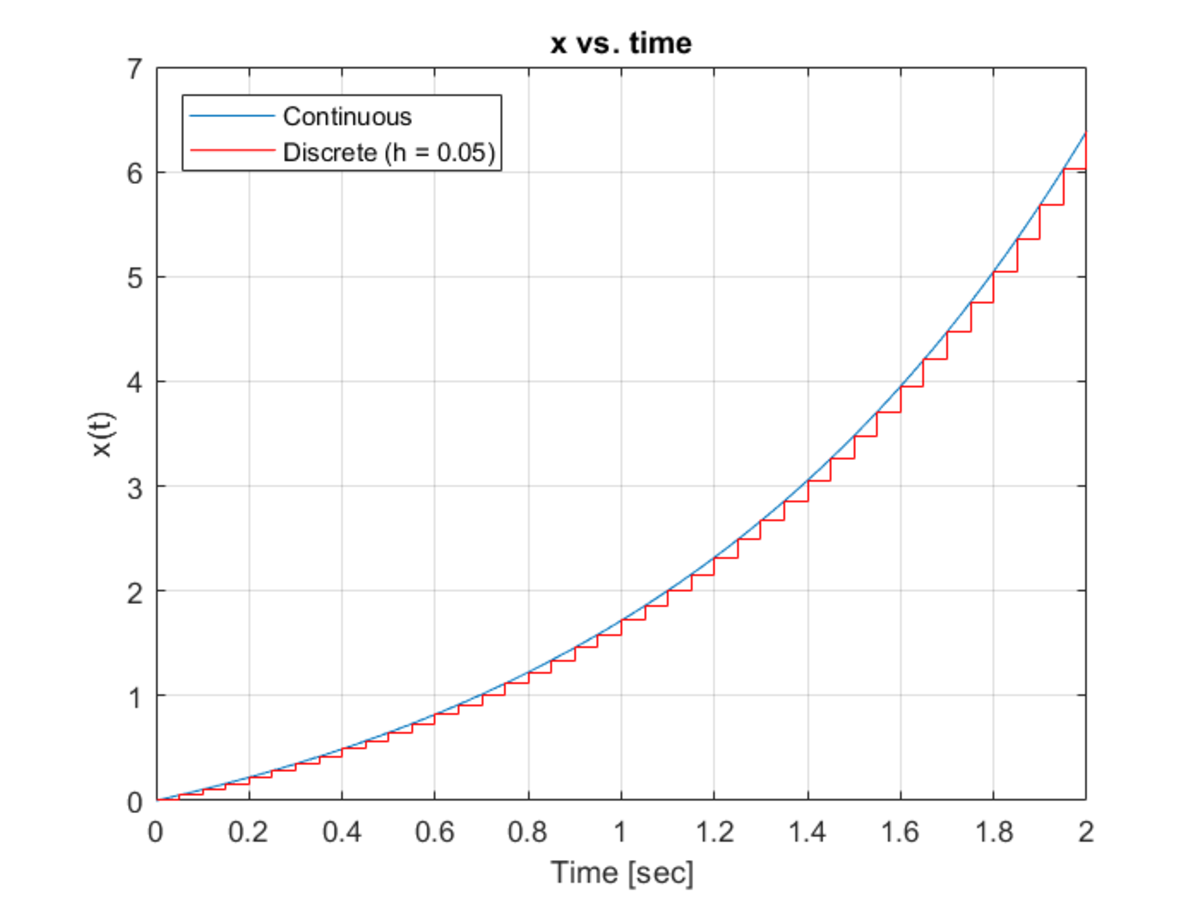
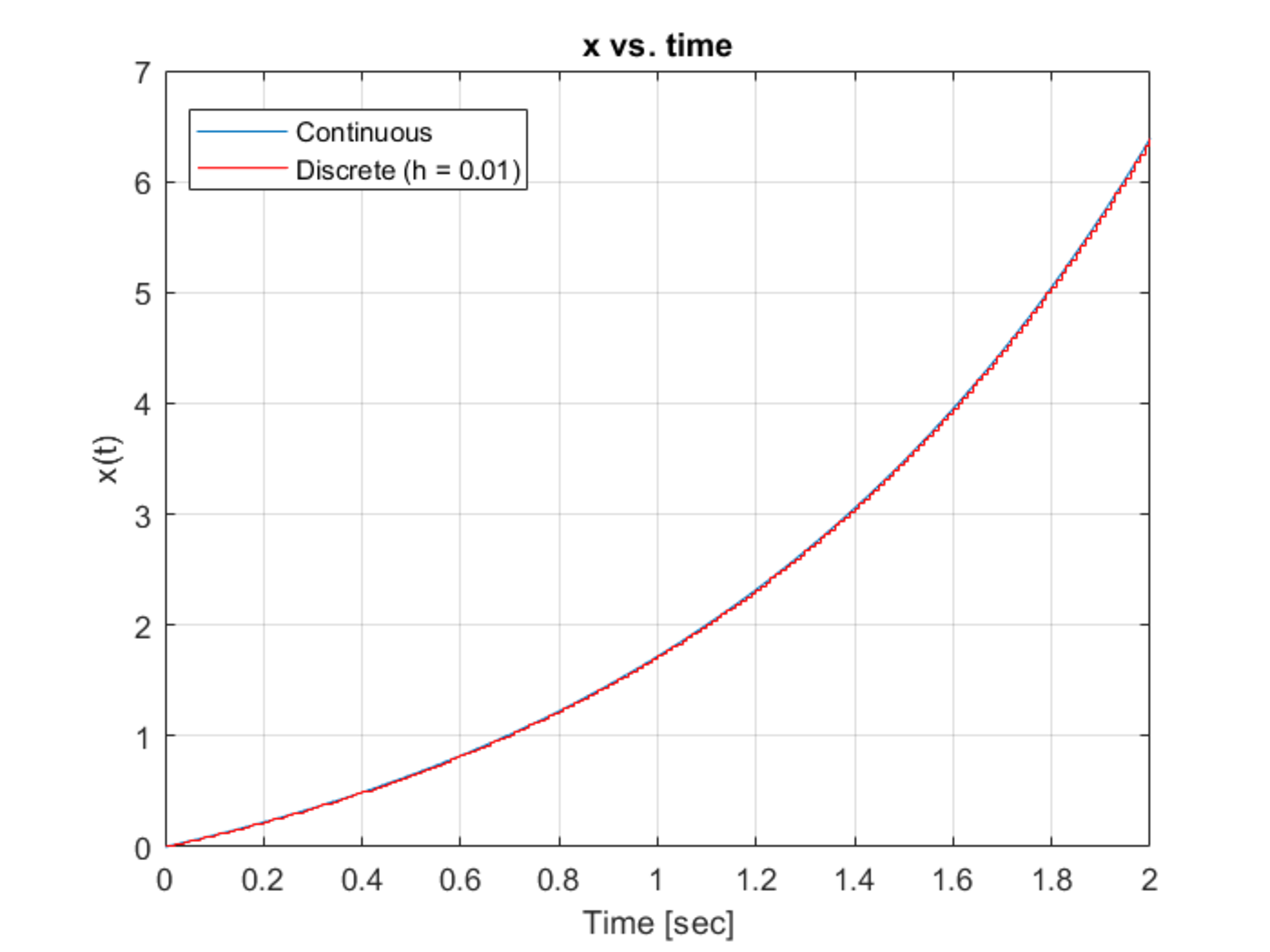
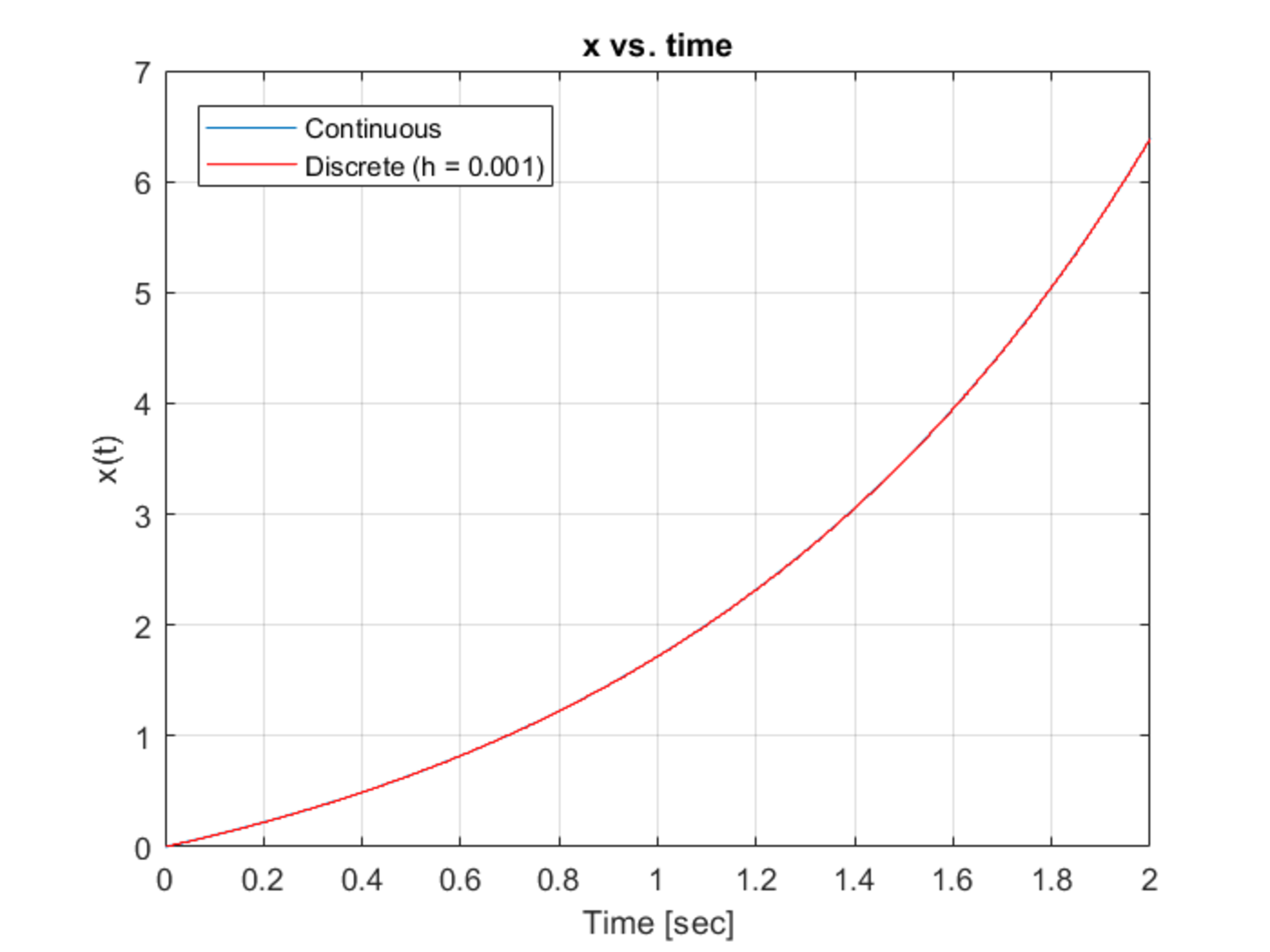
So one can see that $h$ reduces, the discrete-time response comes closer to that of the continuous-time response.

The results derived for a specific dynamic system in this note can be generalized for any linear dynamic system in any number of dimensions. An interested reader may attempt to do so and post his/her comments on this subject.