Coordination Compounds

I had an acquaintance with this question of coordination compounds which I find difficult to solve:

We have a coordination compound of ML $_3$ type structure where the ligand L is .

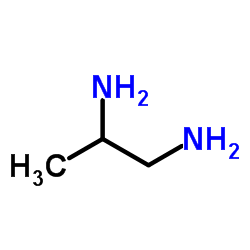Now find the total number of stereoisomers.

Please help me through this problem!

#Chemistry

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

The ligand $L$ stated above is a methyl substituted derivative of ethylenediamine ( $\ce {NH2 - CH2 - CH2 - NH2}$ or $\ce {en}$ ). This ligand is a bidentate chelating ligand where both the nitrogen atoms donate their electrons to the metal ion. Thus the ligand has a coordination number $6$ and not $3$ and it looks like a propeller, like this example

$A complex of $\ce {[Fe (Me-en)3]}^{3+}$$ A complex of $\ce {[Fe (Me-en)3]}^{3+}$

As you can see this has three chiral centers and no restricted rotation sites. So by using the three formulas of finding the number of stereoisomers when number of chiral centers is odd as listed below

$\begin{aligned} & \text{No. of enantiomers } = 2^{n-1} - 2^{{(n-1)}/{2}} \\ & \text{No. of meso compounds } = 2^{{(n-1)}/{2}} \\ & \text{No. of optical stereoisomers } = 2^{n-1} \end{aligned}$

We respectively get

$\begin{aligned} & \text{No. of enantiomers } = 2 \\ & \text{No. of meso compounds } = 2 \\ & \text{No. of optical stereoisomers } = 4 \end{aligned}$

Tapas Mazumdar - 4 years ago

That's true but I faced problem in counting the cases of geometrical isomers in each case above.

Sai Krishna Attaluri - 4 years ago

Is my answer correct? Do you know what the answer is? I didn't make a count btw, just went with the formula.

Tapas Mazumdar - 4 years ago

@Tapas Mazumdar – The answer is 24 stereoisomers. Your answer must be correct regarding optical isomers as I had tried it (in another way) and got the same number of optical isomers but I am not certain.

Sai Krishna Attaluri - 4 years ago

@Sai Krishna Attaluri – Yes, I got the answer. The number of optical isomers is $4$ along with that if you also account the position of methyl group on each ligand, you can have a possible of $6$ configurations wrt position of methyl group, thus $4 \times 6 = 24$ . But this is the total number of all possible isomers.

Tapas Mazumdar - 4 years ago

@Tapas Mazumdar – I will think on this and get back.

Sai Krishna Attaluri - 4 years ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$