Corresponding Angles?
I wanted to prove that here:
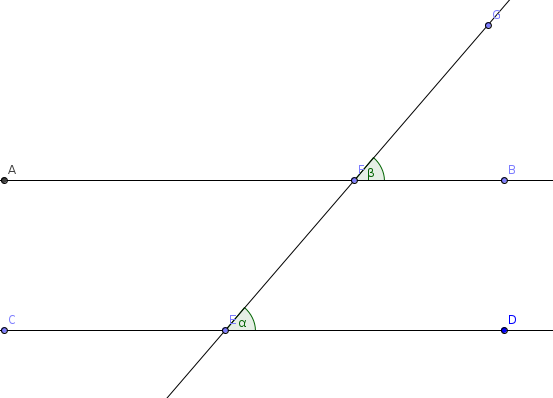 Given .
Given .
The first thing needed was to prove that the distance between the intercepts (rather the vertical distance) remained constant for any value. This can be done using systems of equations easily: You subtract on both sides and are left with , which means that for an value, you will always have a result of the difference between and . This proves that, for any domain, the distances between the two lines will remain the same.
Discounting, for a moment, an extraneous or general transversal, let us start with two cases perpendicular to the x-axis on a Cartesian grid:
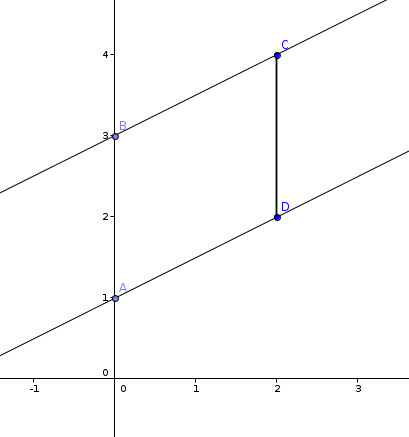 We have already proven above that , now we can show that
with the Pythagorean theorem if we construct a right triangle making the respective line segments the hypotenuses:
We have already proven above that , now we can show that
with the Pythagorean theorem if we construct a right triangle making the respective line segments the hypotenuses:
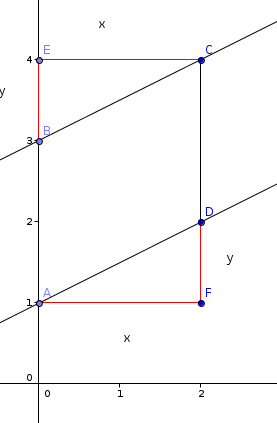
Taking the square root, you can see that they are also congruent.
Next, we can show that the perpendicular case holds true:
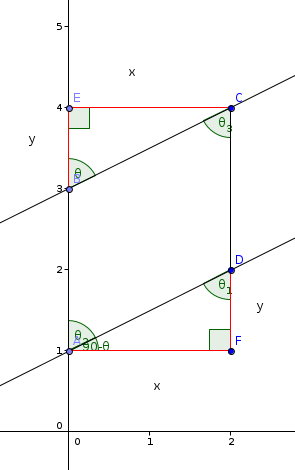 To best show this, you can construct a line segment
With the predetermined congruence and the SSS postulate, this can be show to be true. This means also that:
By the definition of a rectangle, .
To best show this, you can construct a line segment
With the predetermined congruence and the SSS postulate, this can be show to be true. This means also that:
By the definition of a rectangle, .
Taking away everything now immaterial, we see that the corresponding angles theorem is true for the perpendicular case:
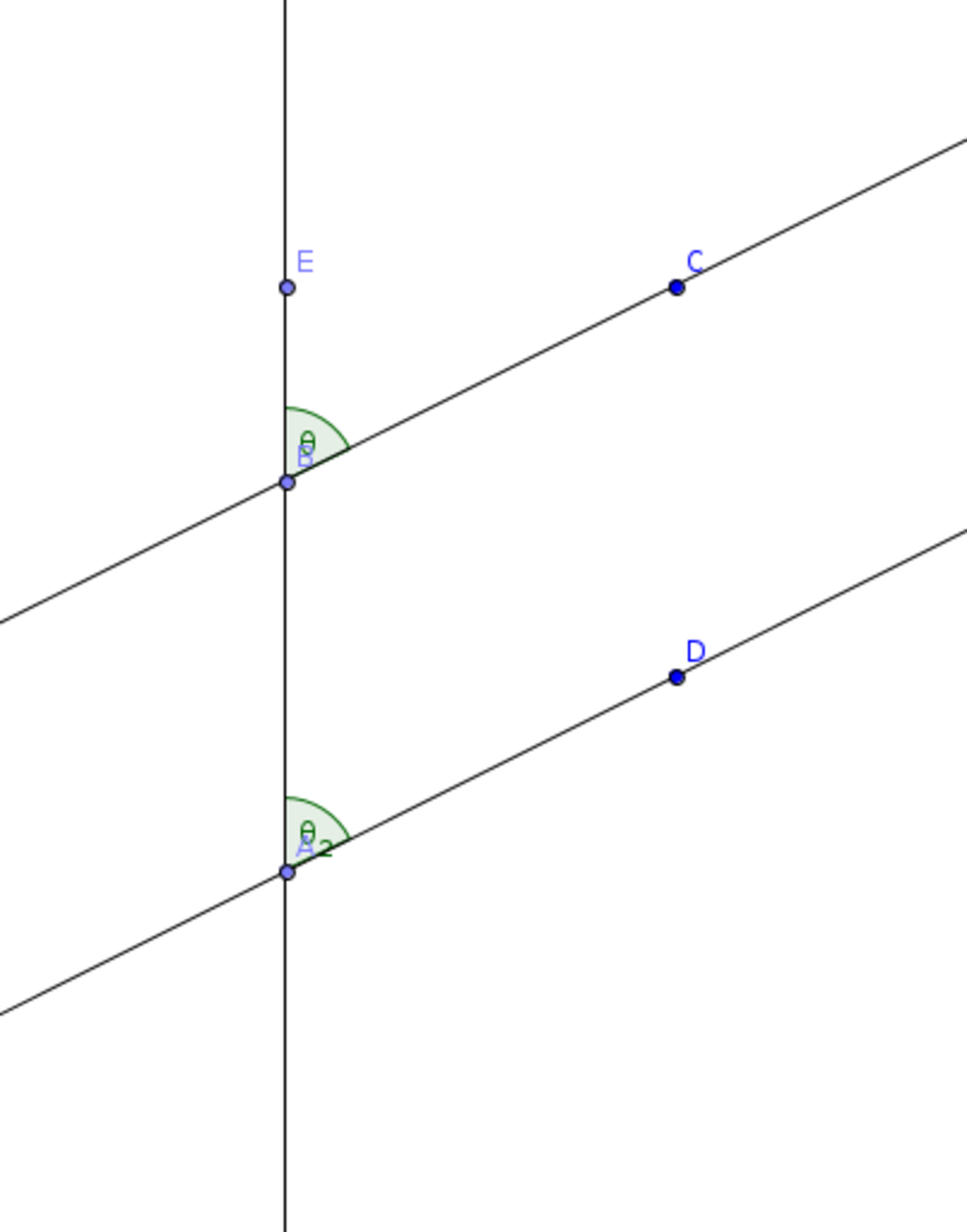
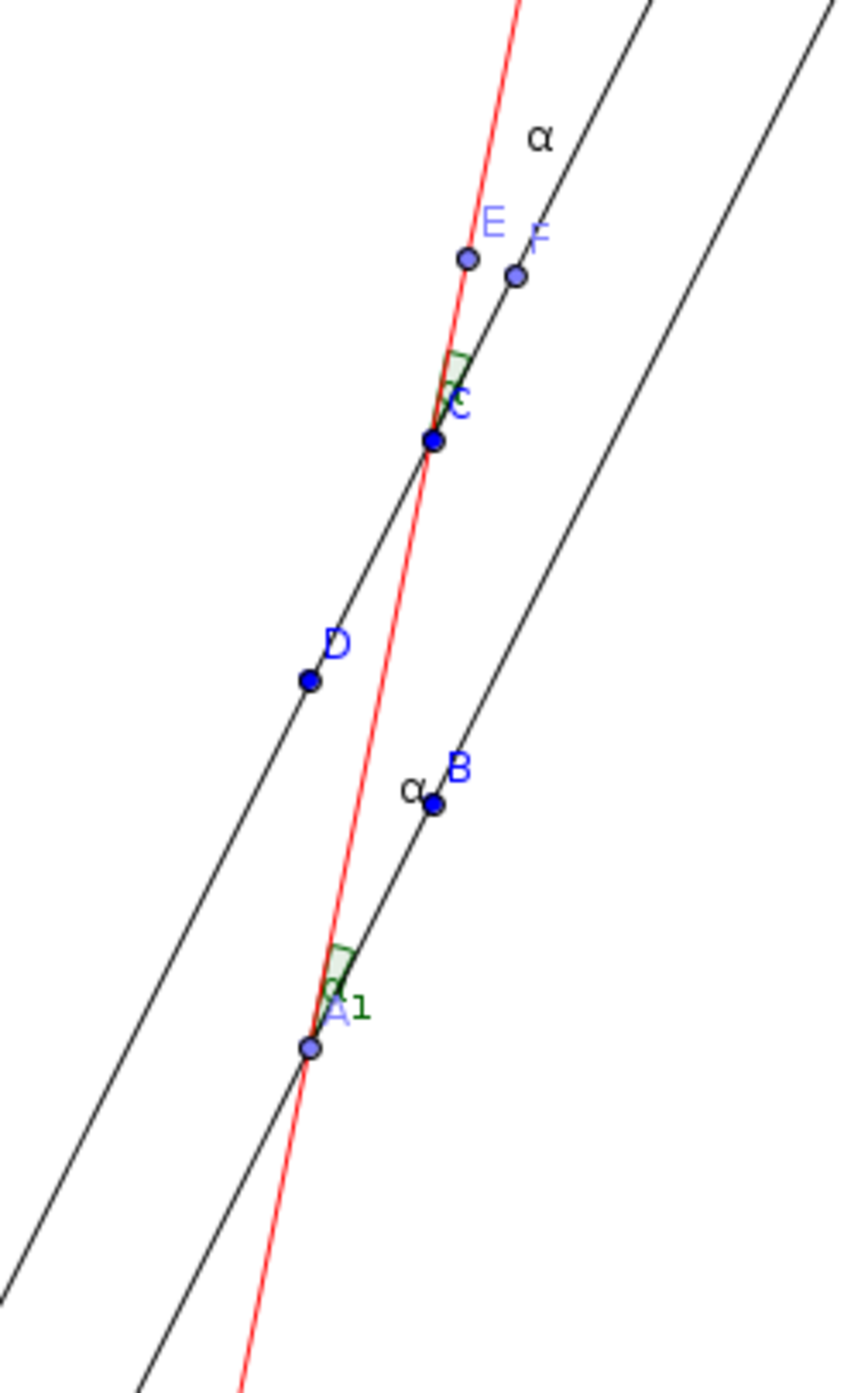
How do we now establish the theorem for all cases? Recall that we have already shown that for any value, we can construct a congruent parallelogram. Becuase the Cartesian coordinate system is relative, we can center it so that our transversal touches the bottom left and top right corners of the parallelogram for any transversal. Here is an example:
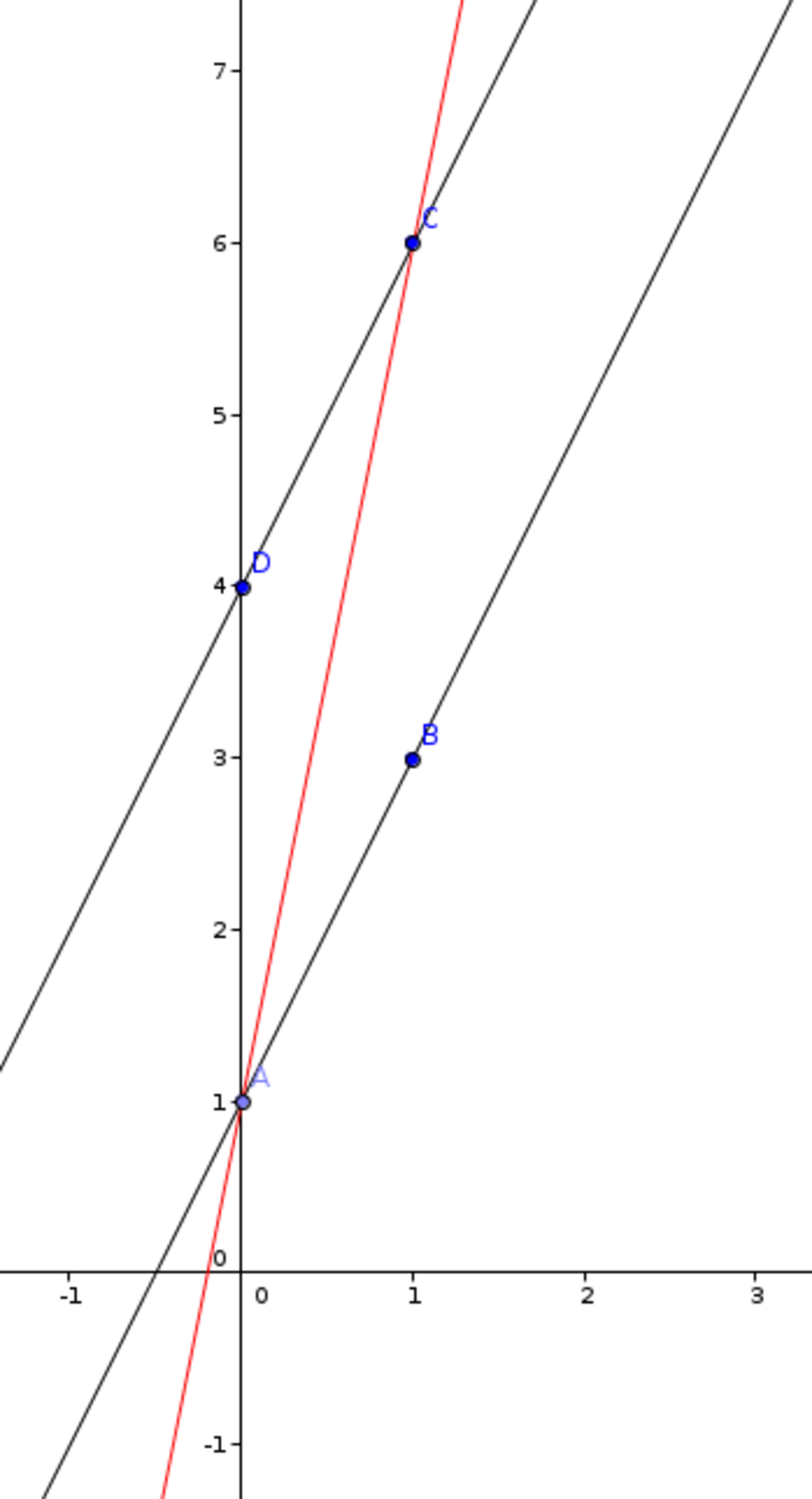 We can again construct the parallelogram as before with the special case:
We can again construct the parallelogram as before with the special case:
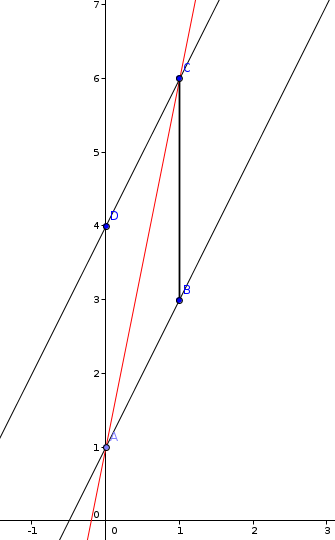 Established previously, we know and . Rather perspicaciously, we know also .
And again, by SSS, .
Established previously, we know and . Rather perspicaciously, we know also .
And again, by SSS, .
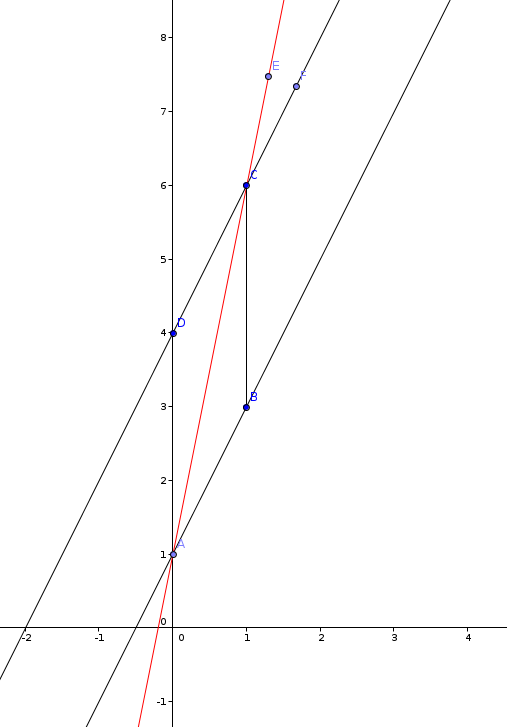 Simple Euclidean geometry will tell you, then, that .
The product is realized when we again clear the excess:
Simple Euclidean geometry will tell you, then, that .
The product is realized when we again clear the excess:
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
You could just draw line BD.Then we have a+180−b=180,a−b=0,a=b