Could it be Possible ? Maybe Confusion
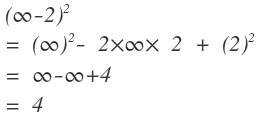
I was scribbling in my note yesterday, when I thought to write something about infinity algebraic expressions. After many tried sums, I had found out a very strange expression in my note.
As I tried to solve it, I saw something very keen and interesting which is in the image.
Is it true ? I too don't think so, but think maybe could be true Like if agree. . Share if you find confusing and interesting or disagree
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
The fallacy is that ∞ is not a number and does not follow the laws of algebra.
Otherwise, ∞=∞+1⟹1=0, which is obviously not true.
Infinity is a concept not a number. Thus it cannot be treated as a number. And also two infinitys are never equal.
Log in to reply
I perfectly agree with you. There may be infinite types of infinities
If you go by the standard Set Theory, there are like 5 useful types of infinities. For example set of natural numbers is of the same size as the set of all primes.
You are absolutely true . There are many types of infinities like in various sequences.
∞ ^2 is not ∞
Log in to reply
It is
Log in to reply
OK I didn't know.
infinity is concept of numbers but it can't be defined so it's not true
infinity -infinity is not 0
It is not true. I don't understand what is it .
Infinity isn't a number,its a thing you may say,so you can't treat it as a number
Check into the Hilbert Hotel.
infinity - infinity is not 0
It's = Infinity Because Infinity is a concept not a number. Thus it cannot be treated as a number. And also two infinitys are never equal.
Here two things are wrong ..
2 . ∞−∞ is not defined , it is an indeterminate form.
No
I don't exactly know how Infinity works but my teacher once told me that infinity minus infinity is not 0
You have done wrong calculation.
This reminds me of myself back then. No, infinity is an idea/concept. There's no way you can treat it as a number, thus you can't solve it.
Cheers!
infinity is something , which is taken sometimes for FOR DOES NOT EXIST condition or sometimes when we take a very large no.
your 2 infinites are not equal in the second line {unless infintiy is 4, which clearly it isnt as it isnt a fixed number}
Here lies the fallacy... infinity is a relative concept...its not an absolute number...hence it fails to satisfy laws of algebra...
Infinity is used to indicate very large number which we can't even imagine. It is a theoretical concept.
I agree with the others - infinity is a concept, not a number.
But aren't you contradicting your own statement? If [(infinity)^2 = infinity] and [-2infinity2 = infinity], then isn't infinity-2 = infinity??
Thanks for getting me right !
Lets consider infinite as n for simpler conventions to facilitate operations ...so n is large no. n^2 is of even larger order we cannot add them both as they are of diff orders /or subtract them.
If you do what is in the brackets first you get ∞^2... which is still ∞
∞−∞=0
so you can't do like that !!!