Derivative of The Sine Function

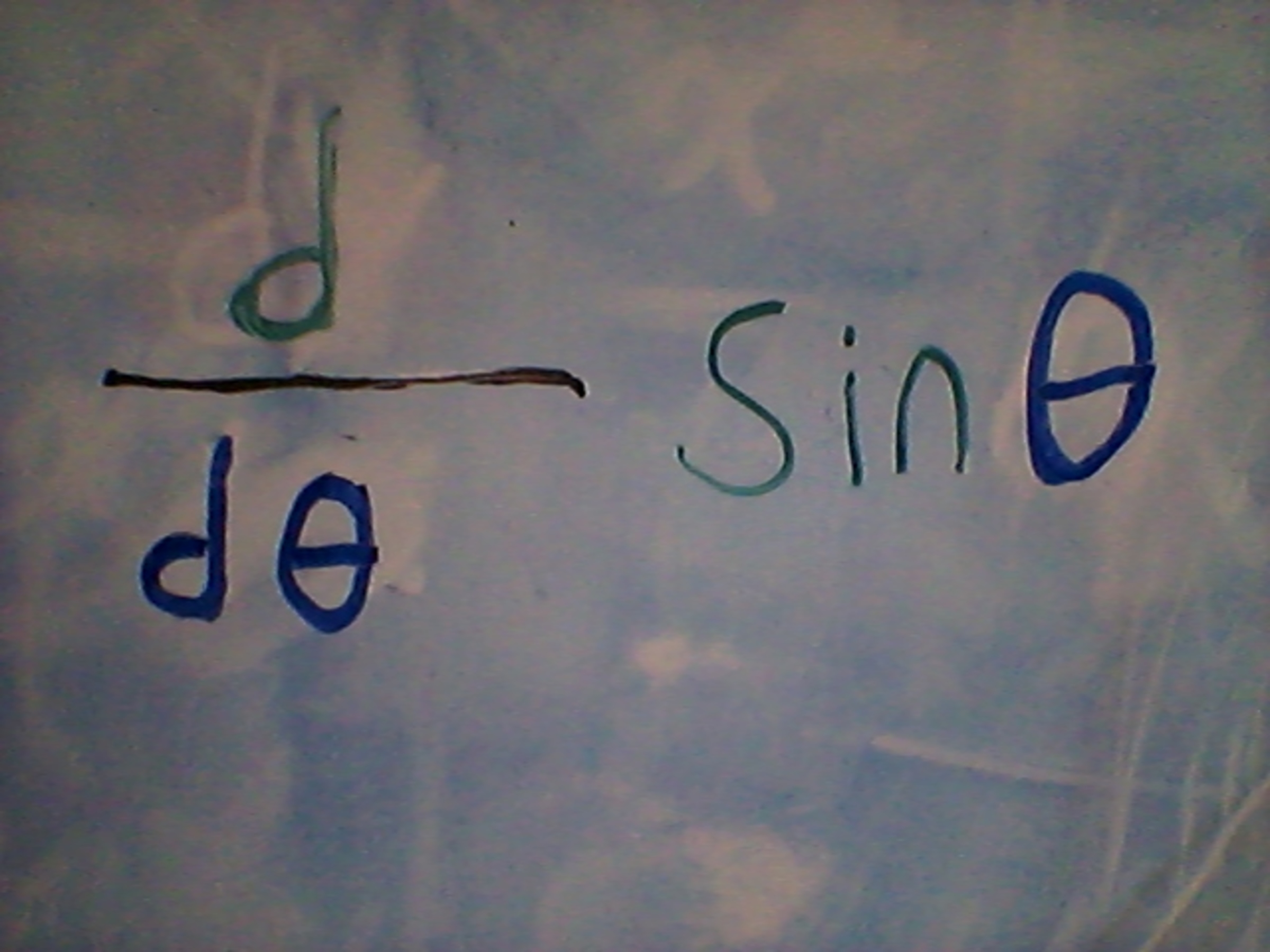
In my last note I proved that lim⁡θ→0θsinθ=1 \quad\displaystyle \lim_{\theta\to 0}\frac { \theta}{sin\theta} = 1

If you have not read that I would recommend reading that first as this limit is used in proving the derivative of the sine function. Here is the link.

lim⁡θ→0θsinθ=? \qquad \qquad\qquad\qquad\qquad\qquad \displaystyle \lim_{\theta\to 0}\frac { \theta}{sin\theta} = ?

To prove the derivative of the sine function we will be using the first principles of derivatives.

lim⁡Δθ→0sin⁡(θ+Δθ)−sin⁡θΔθ\qquad\qquad\qquad\qquad\qquad\displaystyle \lim_{\Delta\theta\to 0}\frac{\sin(\theta + \Delta\theta) - \sin\theta}{\Delta\theta}

Use the addition formula for sin⁡(θ+Δθ)\sin(\theta + \Delta\theta).

=lim⁡Δθ→0sin⁡θ×cos⁡Δθ+sin⁡Δθ×cos⁡θ−sin⁡θΔθ=\qquad\qquad\qquad\quad\displaystyle\lim_{\Delta\theta\to 0} \frac{\sin\theta \times \cos \Delta\theta + \sin\Delta\theta \times \cos\theta - \sin\theta}{\Delta\theta}

rearrange the equation and factor out sin⁡θ\sin\theta

=lim⁡Δθ→0sin⁡θ×cos⁡Δθ−sin⁡θ+sin⁡Δθ×cos⁡θΔθ=\qquad\qquad\qquad\quad\displaystyle\lim_{\Delta\theta\to 0} \frac{\sin\theta \times \cos \Delta\theta - \sin\theta + \sin\Delta\theta \times \cos\theta }{\Delta\theta}

=lim⁡Δθ→0sin⁡θ(cos⁡Δθ−1)+sin⁡Δθ×cos⁡θΔθ=\qquad\qquad\qquad\quad\displaystyle\lim_{\Delta\theta\to 0} \frac{\sin\theta( \cos \Delta\theta - 1) + \sin\Delta\theta \times \cos\theta }{\Delta\theta}

break apart the fraction

=lim⁡Δθ→0sin⁡θ(cos⁡Δθ−1)Δθ+sin⁡Δθ×cos⁡θΔθ=\qquad\qquad\qquad\quad\displaystyle \lim_{\Delta\theta\to 0}\frac{\sin\theta( \cos \Delta\theta - 1)}{\Delta\theta} + \frac{\sin\Delta\theta \times \cos\theta }{\Delta\theta}

=lim⁡Δθ→0sin⁡θ×(cos⁡Δθ−1)Δθ+sinΔθΔθ×cosθ=\qquad\qquad\qquad\quad\displaystyle \lim_{\Delta\theta\to 0}\sin\theta \times \frac{( \cos \Delta\theta - 1)}{\Delta\theta} + \frac{sin\Delta\theta}{\Delta\theta} \times cos\theta

We wIll now evaluate the two limits seperately

lim⁡Δθ→0sinΔθΔθ×cosθ\qquad\qquad\qquad\quad\displaystyle \lim_{\Delta\theta\to 0} \frac{sin\Delta\theta}{\Delta\theta} \times cos\theta

In my last note I proved that lim⁡Δθ→0sinΔθΔθ=1\displaystyle\lim_{\Delta\theta\to 0}\frac{sin\Delta\theta}{\Delta\theta}=1

=lim⁡Δθ→01×cosθ=\qquad\qquad\qquad\quad\displaystyle \lim_{\Delta\theta\to 0} 1 \times cos\theta

=lim⁡Δθ→0cosθ=\qquad\qquad\qquad\quad\displaystyle \lim_{\Delta\theta\to 0} cos\theta

That solves that limit now the other limit.

lim⁡Δθ→0sin⁡θ×(cos⁡Δθ−1)Δθ\qquad\qquad\qquad\quad\displaystyle \lim_{\Delta\theta\to 0}\sin\theta \times \frac{( \cos \Delta\theta - 1)}{\Delta\theta}

divide out the sin⁡θ\sin\theta

=sin⁡θlim⁡Δθ→0(cos⁡Δθ−1)Δθ=\qquad\qquad\qquad\quad\displaystyle \sin\theta \lim_{\Delta\theta\to 0} \frac{( \cos \Delta\theta - 1)}{\Delta\theta}

multiply by the conjugate

=sin⁡θlim⁡Δθ→0(cos⁡Δθ−1)Δθ×cos⁡Δθ+1cos⁡Δθ+1=\qquad\qquad\qquad\quad\displaystyle \sin\theta \lim_{\Delta\theta\to 0} \frac{( \cos \Delta\theta - 1)}{\Delta\theta} \times \frac{\cos\Delta\theta+1}{\cos\Delta\theta+1}

=sin⁡θlim⁡Δθ→0(cos⁡2Δθ−1)Δθ(cos⁡Δθ+1)=\qquad\qquad\qquad\quad\displaystyle \sin\theta \lim_{\Delta\theta\to 0} \frac{( \cos^{2} \Delta\theta - 1)}{\Delta\theta(\cos\Delta\theta+1)}

Rewrite the the equation using the Pythagorean identity. cos⁡2θ+sin⁡2θ=1 \cos^{2}\theta + \sin^{2}\theta=1

=sin⁡θlim⁡Δθ→0−sin⁡2ΔθΔθ(cos⁡Δθ+1)=\qquad\qquad\qquad\quad\displaystyle \sin\theta \lim_{\Delta\theta\to 0} \frac{-\sin^{2} \Delta\theta }{\Delta\theta(\cos\Delta\theta+1)}

break apart the fraction

=sin⁡θlim⁡Δθ→0(−sinΔθ)×sin⁡ΔθΔθ×1cos⁡Δθ+1=\qquad\qquad\qquad\quad\displaystyle \sin\theta \lim_{\Delta\theta\to 0} (-sin\Delta\theta) \times \frac{\sin\Delta\theta}{\Delta\theta} \times \frac{1}{\cos\Delta\theta + 1}

evaluate the limits

=sin⁡θ×(−sin0)×1×1cos⁡0+1=\qquad\qquad\qquad\quad\displaystyle \sin\theta \times (-sin0) \times 1 \times \frac{1}{\cos0 + 1}

=sin⁡θ×0×1×12=\qquad\qquad\qquad\quad\displaystyle \sin\theta \times 0 \times 1 \times \frac{1}{2}

=0=\qquad\qquad\qquad\quad\displaystyle 0

Now add both limts.

ddθ=lim⁡Δθ→0sin⁡θ×(cos⁡Δθ−1)Δθ+lim⁡Δθ→0sinΔθΔθ×cosθ \displaystyle \frac{d}{d\theta}=\qquad\qquad\qquad\quad \lim_{\Delta\theta\to 0}\sin\theta \times \frac{( \cos \Delta\theta - 1)}{\Delta\theta} + \lim_{\Delta\theta\to 0}\frac{sin\Delta\theta}{\Delta\theta} \times cos\theta

ddθ=0+cos⁡θ \displaystyle \frac{d}{d\theta}=\qquad\qquad\qquad\quad0 + \cos\theta

ddθ=cos⁡θ \displaystyle \frac{d}{d\theta}=\qquad\qquad\qquad\quad \cos\theta

#Calculus #Derivatives #DerivativeByFirstPrinciple

Note by Brody Acquilano
6 years, 1 month ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

There are no comments in this discussion.

×

Problem Loading...

Note Loading...

Set Loading...