Did I find out something in my dreams? (I)

One day, I was asleep, and in my dream yesterday, I dreamt that I was playing with factorials. I then got this sudden revelation of a weird formula:

$\LARGE{\frac{1! × 2! × ... × n!}{1 × 2 × ... × 2n}}$

Simplifying this, we can get:

$\LARGE{\frac{G(n + 2)}{(2n)!}}$

Where $G(z)$ is the $\text{Barnes G-function}$ and $G(n + 2)$ is the superfactorial

When we substitute $n$ with different values, we gain these numbers:

$n = 3$	$0.01666…$
$n = 4$	$0.00714285…$
$n = 5$	$0.00952380…$
$n = 6$	$0.0519480…$
$n = 7$	$1.438561…$

I decided to plot this using WolframAlpha, but I do not have the Pro Version, so I plotted a smaller range of values instead (because I was bored a lot...)

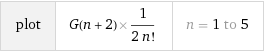
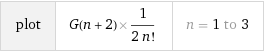
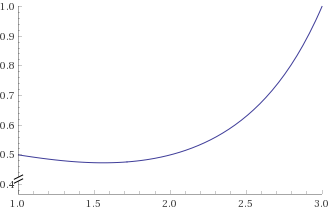
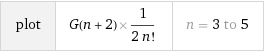
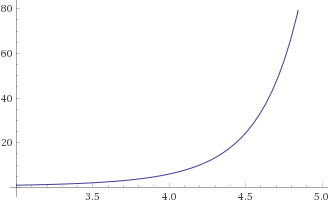
Does this graph or number set have any special value to them? I was just bored, but maybe you can find a better explanation for these numbers. I would love to see what random facts you can gain about these weird numbers that came to me in a dream...

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Did I find out something in my dreams? (I)

Comments