Discovery of Irrational Numbers

Square Root of 2 Diagram

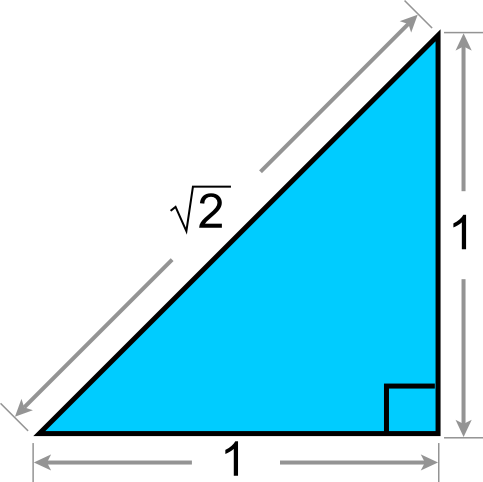
The first man to recognize the existence of irrational numbers might have died for his discovery. Hippassus of Metapontum was an Ancient Greek philosopher of the Pythagorean school of thought. Supposedly, he tried to use his teacher's famous theorem $a^{2}+b^{2}= c^{2}$ to find the length of the diagonal of a unit square. This revealed that a square's sides are incommensurable with its diagonal, and that this length cannot be expressed as the ratio of two integers. The other Pythagoreans believed dogmatically that only positive rational numbers could exist. They were so horrified by the idea of incommensurability, that they threw Hippassus overboard on a sea voyage, and vowed to keep the existence of irrational numbers an official secret of their sect.

There are good reasons to believe Hippassus's demise is merely an apocryphal myth. The primary sources that refer to the incident are both sparse and written 800 years after the time of Pythagoras and Hippassus. That said, a few ancient accounts and their more contemporary embellishments suggest that one of these likely happened:

Ippaso di Metaponto

• Hippassus of Meropontum (5th century BC), might have followed his curiosity to a watery grave.
• Hippassus discovered irrational numbers on a boat, and his colleagues were so horrified, they threw him overboard.
• Hippassus discovered irrational numbers, the pythagoreans ostracized him, and the gods were so disgusted by his discovery that they scuttled his boat on the high seas.
• Hippassus discovered irrational numbers, he died on an ocean voyage in a natural accident (the sea is a treacherous place). His colleagues were still so displeased with his discovery that they wished they had been the ones to throw him overboard.
• None of the above are true, and they are tales invented and embellished through the ages to illustrate a pivotal moment in history.
• If Hippassus did discover irrational numbers, it is also not certain which method he used to do so. For the curious, the Brilliant summary page on Rational Numbers builds up to Euclid's famously beautiful proof of the irrationality of $\sqrt{2}$. This is one way Hippassus might have done it, however many scholars think Euclid's method(written 300 years after the time of Hippassus) is more advanced than what Hippassus would have been able to do.

Regardless of what actually happened, it is crazy to imagine a time when proving the existence of an irrational number was a mortal transgression.

Humans have had numbers for at least all of recorded history. Our earliest basis for numbers and math derive from the practical need to count and measure things. It is intuitive to see how the positive, non-zero, natural numbers would arise "naturally" from the process of counting. It is also easy to see how measurement would present you with things that could not be divided into whole units, or whose dimensions were in between a whole number. Inventing fractions made practical sense, as ratios of the natural numbers. Discovering the positive rational numbers was probably pretty intuitive.

Numbers may have originated from purely practical needs, but to the Pythagoreans, numbers were also the spiritual basis of their philosophy and religion. Pythagorean cosmology, physics, ethics, and spirituality were predicated on the premise that "all is number." They believed that all things-- the number of stars in the sky, the pitches of musical scales, and even the qualities of virtue, could be described by and apprehended through rational numbers.

This is a 19th century depiction of Pythagoreans celebrating sunrise (Fyodor Bronnikov). The Pythagoreans attributed mystical significance to their ability to perceive the presence of rational numbers in everything, be it a sunrise or a musical harmony.

One reason to think that positive rational numbers would form the basis for all things in the universe is that there is an infinite amount of them. Intuitively, it might seem reasonable that an infinite amount of numbers should be enough to describe anything that might exist. Along the number line, rational numbers are unfathomably “dense”. There is not much “space” between $\frac{1}{100000}$ and $\frac{1}{100001}$, but if you ever needed to describe something between those two numbers you would have no problem finding a fraction between them.

The number line is infinitely dense with rational numbers. The existence of irrational numbers implies that despite this infinite density, there are still holes in the number line that cannot be described as a ratio of two integers.

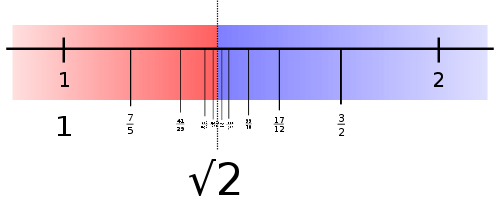
The number line is infinitely dense with rational numbers. The existence of irrational numbers implies that despite this infinite density, there are still holes in the number line that cannot be described as a ratio of two integers.

The Pythagoreans had probably manually measured the diagonal of a unit square before. They probably regarded the measurement as an approximation, that was close to a precise rational number that must be the true length of the diagonal. Before Hippassus, they had no reason to suspect that there are logically real numbers that in principle, not merely in practice, cannot be measured or counted to.

If you believed that all numbers are rational numbers, and that rational numbers are the basis of all things in the universe, then having something that cannot be expressed as the ratio of two integers is like discovering a gaping void in the universe. An irrational number was a blight of meaninglessness on what up until then had seemed like an orderly world. The Pythagoreans wanted numbers to be something you could count on, and for all things to be counted as rational numbers. The discovery of an irrational number proved that there existed in the universe things that could not be apprehended through rational numbers, threatening not only Pythagorean mathematics, but their philosophy as well.

Feel free to share your thoughts on the discussion page.

Sources:

History of Mathematics, Volumes I and II, D.E Smith, 1953.

A History of Greek Mathematics- Volume I from Thales to Euclid, Sir Thomas Heath, 1921.

The Irrationals: A Story of the Numbers You Can't Count on, Julian Havil, 2012.