Discussion: The Prismoidal Formula

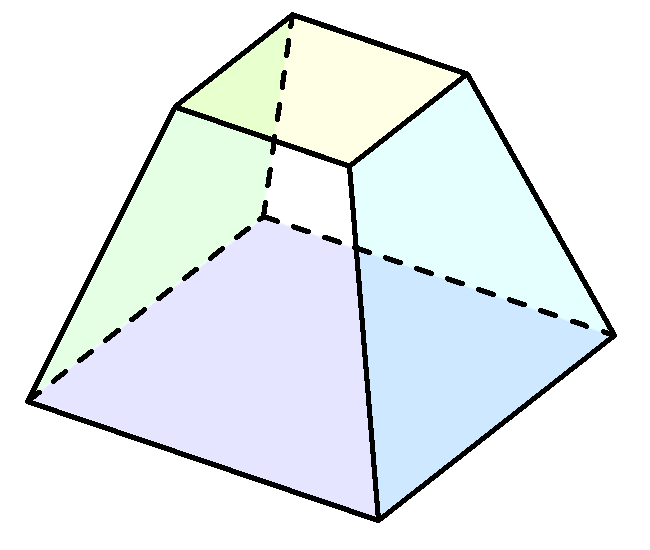
A prismatoid(a.k.a. prismoid) is a solid where all vertices lie on two parallel planes. According to the prismoidal formula, the volume can be calculated by this simple equation \[V = \frac{h}{6} \left({A}_{T} + 4{A}_{M} + {A}_{B}\right )\] where $h$ denotes the height, and ${A}_{T}$, ${A}_{M}$, ${A}_{B}$ are the top, middle and bottom cross-sectional areas respectively.

However, the prismoidal formula is not a universal formula for computing the volumes of solids. Since the prismodal formula is actually Simpson's rule, the prismatoid formula is precise if the shape is bounded by a polynomial function up to degree three. This can be proven via Lagrange error bounds Error bound of Simpson's Rule.

Check out my other notes at Proof, Disproof, and Derivation

#Geometry #Calculus #LagrangeErrorBounds #Simpson'sRule

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

can you determine the parts of prismatoid?

Nezthiel Mejos - 6 years, 4 months ago

What do you mean by determine?

Steven Zheng - 6 years, 4 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$