Dividing a Circle into the Maximum Number of Regions with n lines

Recently, I came across a question that required to find the maximum number of regions a circle can be divided into with 4 lines, considering regions fromed inside the circle only. The question was an easy one; a fair bit of trial-and-error popped out the answer as 1111. But what if there were, let's say, 100100 lines? Obviously, trial-and-error here would drain the soul out of me! So, I started investigating the mechanism that created the maximum number of regions for nn lines, and derived a formula which would give us the answer directly.

First of all, I found that when I was trying for the n=4n=4 case, what I was essentialy trying to do is to make sure that every new line I drew cut all the previous lines, thereby forming the maximum regions. To put it in another way, I sought to draw the nthn^{th} line such that it cut all the previous n−1n-1 lines.

After this realization, I tried to find out the number of regions that were being added after each new line was drawn. For example, when the first line is drawn, 22 regions are formed.

When the second line is drawn, 22 more regions are added to the figure. The regions shaded red are the newly added regions.

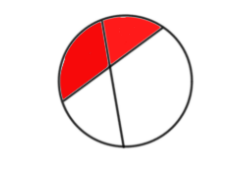
When the third line is drawn cutting the previous 22 lines, 33 more regions are added.

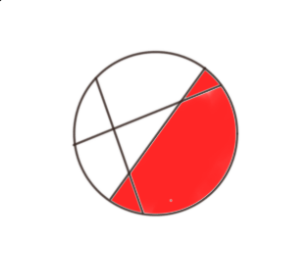
When the fourth line is drawn cutting the previous 33 lines, 44 more regions are formed.

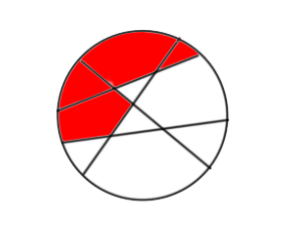
Thus, we have now found out a pattern.

Generalizing, the addition of the nthn^{th} line results into the formation of nn new regions. This is because when you draw the nthn^{th} line cuting the previous n−1n-1 lines, you add a total of n−1+1=nn-1+1 = n regions.

This pattern can now be condensed into an Arithmetic Progression whose nthn^{th} term represents the number of regions that are being added as each new line is drawn.

1st2nd3rd4th5thnth
22345n

Note that all terms except the first one are a part of this AP with common difference 11, so we add it separately. The total total number of terms in this AP are n−1n-1. The first term is 22. Apply the formula for the sum of an AP.

Maximum regions formed:

2+(n−1)2×[4+(n−2)×1]2 + \dfrac{(n-1)}{2}\times [4+ (n-2)\times 1]

= 2+(n−1)2(n+2) 2 + \dfrac{(n-1)}{2}(n+2)

= 4+n2+n−22\dfrac{4 + n^2 + n - 2}{2}

= n2+n+22\boxed{\dfrac{n^2 + n + 2 }{2}}

#Geometry

Note by Anuj Shikarkhane
2 years, 6 months ago

No vote yet
1 vote

  Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

  • Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
  • Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
  • Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
  • Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

MarkdownAppears as
*italics* or _italics_ italics
**bold** or __bold__ bold

- bulleted
- list
  • bulleted
  • list

1. numbered
2. list
  1. numbered
  2. list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)example link
> This is a quote
This is a quote
    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"
# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"
MathAppears as
Remember to wrap math in \( ... \) or \[ ... \] to ensure proper formatting.
2 \times 3 2×3 2 \times 3
2^{34} 234 2^{34}
a_{i-1} ai−1 a_{i-1}
\frac{2}{3} 23 \frac{2}{3}
\sqrt{2} 2 \sqrt{2}
\sum_{i=1}^3 ∑i=13 \sum_{i=1}^3
\sin \theta sin⁡θ \sin \theta
\boxed{123} 123 \boxed{123}

Comments

I think your table had a slight error. 1st line adds 1 region. (There is one region inside a circle with no lines, the first line splits this in two, so one is added)

Also, your 3rd picture makes no sense.

Nice formula, though.

Jeremy Galvagni - 2 years, 5 months ago
×

Problem Loading...

Note Loading...

Set Loading...