Dividing Line Segments in Affine Geometry

Here are the steps to divide a line segment into $n$ equal segments using only the tools in affine geometry. Here, we assume the axiom that there is a unique line through a given point that is parallel to a given line, i.e. the two lines do not meet.

1. Construct the line segment $\overline{AB}$, given points $A$ and $B$ in affine $n$-space.

2. Take one of the points on the line segment, say $A$, and draw a line through $A$ not parallel to the line $AB$.

3. Pick a point $C_1$ on the line constructed in Step 2.

4. Draw a line through $A$ not parallel to the line $AB$ or $AC_1$, and pick a point $D_1$ on this line.

5. Construct a parallel line to the line $AC_1$ through the point $D_1$.

6. Construct a parallel line to the line $AD_1$ through the point $C_1$, and define the meet (intersection) of this line with the line in Step 4 to be the point $D_2$.

7. Draw the line $D_1C_1$ and construct a parallel line to this line through the point $D_2$.

8. Define $C_2$ to be the meet of the line constructed in Step 6 with the line $AC_1$.

9. Repeat Steps 5-7, now with $C_1$, $C_2$ and $D_2$ instead of $A$, $C_1$ and $D_1$; we do this $n-1$ times, so that we get $n$ copies of the line segment $\overline{AC_1}$.

10. Suppose then that the last point we have is $C_n$; we then draw the line $BC_n$.

11. Through each of the points $C_i$, for $i$ ranging from $1$ to $n-1$, draw the lines through each of the points, parallel to the line drawn in Step 9.

12. The meets of each of the lines in Step 10 and the line segment $\overline{AB}$ will then be denoted by $E_i$, for $i$ ranging from $1$ to $n-1$.

As a result of this construction, we then have that the points $E_i$, for $i$ ranging from $1$ to $n-1$, divide the line segment $\overline{AB}$ into $n$ equal line segments.

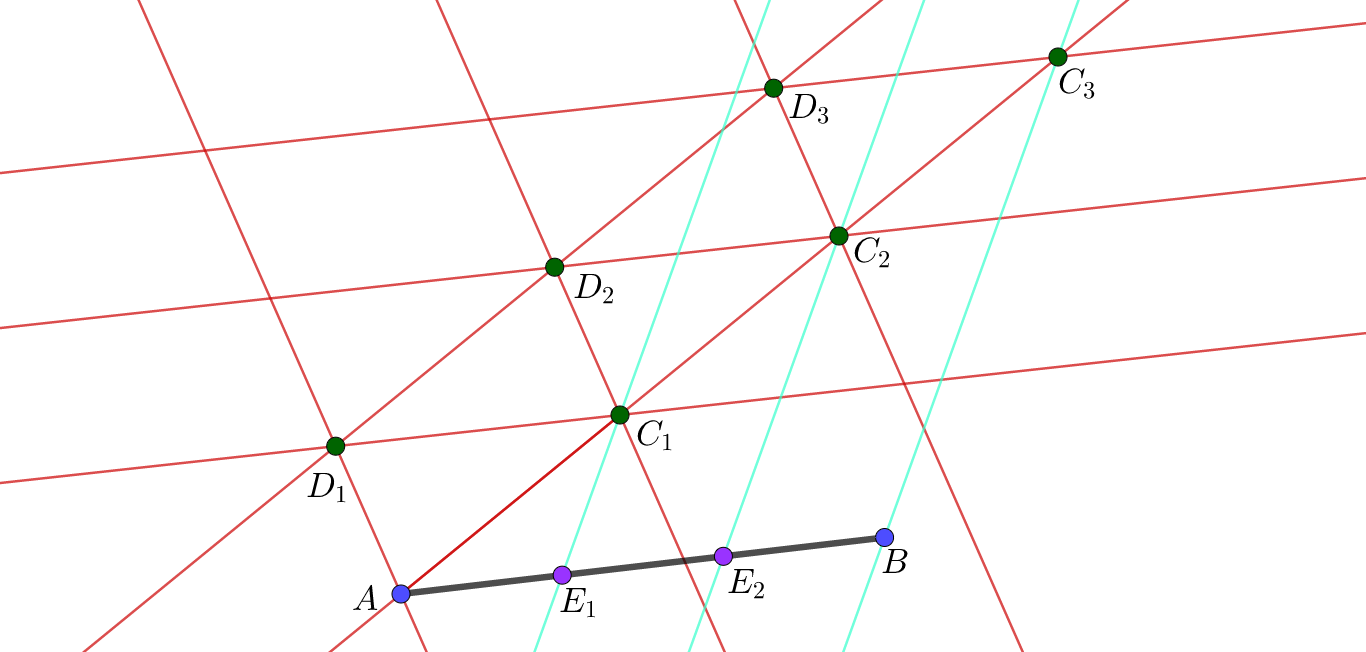
I did a construction (see picture above) where I just divided a simple line segment into $3$ equal segments.

EDIT: Picture too small to look at by eye; not sure how to make it bigger. Just click to enlarge, I guess.

EDIT 2: There are a lot more things to say about this, but I am going to write a book with this content in it. Don't want to spoil too much...