Doubt in a certain category of Physics problems

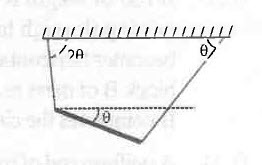
Find the angular acceleration and the tension in the left string just after the right string in cut.

I dont have much clarity on how to solve the above type of problems. Could anyone post a detailed solution to this?

#Rotation #Physics #RotationalMotion #HelpMe! #Help

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Milun is absolutely correct. To be more specific consider these general equations:

$mg - T_{v} = ma$ , where $T_{v}$ is the vertical component of the tension.

$\sum \tau_{CM} = I_{CM} \alpha$ i.e., sum of torque of all the forces about the center of mass(only) = $I\alpha$

For the third and the last equation, the constraint equation, consider the point on the rod attached to the left string (i.e. the end of the string which is not attached to the ceiling). It cannot have any acceleration as the string is inextensible and one end of the string is fixed. Hence add the accelerations of that point along the string (i.e., components of $\vec{a} \mathrm{and} (\vec{\alpha} \times \vec{r}$ ) along the string) as vectors and equate the sum to zero.

You will end up having three equations and three variables. Solve for them.

Note: Take the torque only about center of mass (just to avoid a careless mistake especially in examination) or if you do take about any axis do be very careful of taking the torque due to pseudo force also.
(so that you don't commit the same mistake which I did when I first solved such type of sum :D)

On a side note, which books would you recommend for practicing good sums for JEE Advanced (especially Physics and Maths) because I am unable to find out one.

Sudeep Salgia - 7 years, 2 months ago

I don't know about any good books but I feel it would be more useful to solve many papers. By solving papers we come across a variety of questions and many concepts also get revised.By the way, did ACP teach you Physics?

Karthik Kannan - 7 years, 2 months ago

Karthik, I agree with you that solving papers would be useful. But what I feel is that solving papers are better for developing exam temperament rather than revision. This is because, in general, the question papers involve questions based on aspects which we frequently come across not on those which we miss by whichever means, lack of practice, or lack of revision. For ACP teaching physics, he taught me only EMI, EM Waves and Magnetism.

Sudeep Salgia - 7 years, 2 months ago

Thank you very much. One more question. what if the string is replaced by a spring? Then, clearly, the spring in extensible. So, will the constraint change?

Anish Puthuraya - 7 years, 2 months ago

In case you are not given $x$ , you can find the tensions in both strings initially by balancing force and torque. Then, as we know that tension in a spring doesn't suddenly change (as $x$ doesn't suddenly change) , we can use this value in our new equations.

jatin yadav - 7 years, 2 months ago

If it is a spring , you will know tension ( $F=kx$ ) and problem would be easy.

jatin yadav - 7 years, 2 months ago

In case of spring, that constraint would no longer be true because spring is extensible. However as Jatin says the tension in the spring is known (from initial conditions). Thus overall the number of equations remains the same and we can solve for various unknowns : )

Karthik Kannan - 7 years, 2 months ago

The only important part of such questions is that using the property of the string to be inextensible. So both ends of the string will have the same acceleration along the string. Just write force equations as well as torque equations and use the above constraint relation. Remember the tension in a string can change rapidly but if of were a spring then tension would have been that as before cuttimg

Milun Moghe - 7 years, 2 months ago

Which two ends are you talking about? The other end of the left string is attached to the wall, so it cant have any acceleration, can it?

Anish Puthuraya - 7 years, 2 months ago

Sorry really mistaken I meant to say the acceleration along the string is zero as one end is fixed

Milun Moghe - 7 years, 2 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$