Doubt on Ronak's Question.

https://brilliant.org/problems/electric-fields-due-to-different-kinds-of-plates/.

The link is given.

Here, while doing with Integration results in different value. I will be glad if someone points out where i am wrong.

QUESTION

We have a triangular uniformly charged plate of charge density $\sigma$ .

We take a point just above a vertex of the triangular plate at a distance $d$ perpendicular to the plane of the triangle. Let the vertical component of electric field at that point be $E(d)$ in $V/m$

Find $\displaystyle \lim_{d \rightarrow 0}{E(d)}$

Details and Assumptions:

1) $\sigma = 10^{-9} C , {\epsilon}_{0}=8.85 \times {10}^{-12} \text{ SI units}$

2) The triangle is equilateral. By vertical component of electric field I mean electric field perpendicular to the plane of charge.

3) The plate is non conducting.

MY SOLUTION

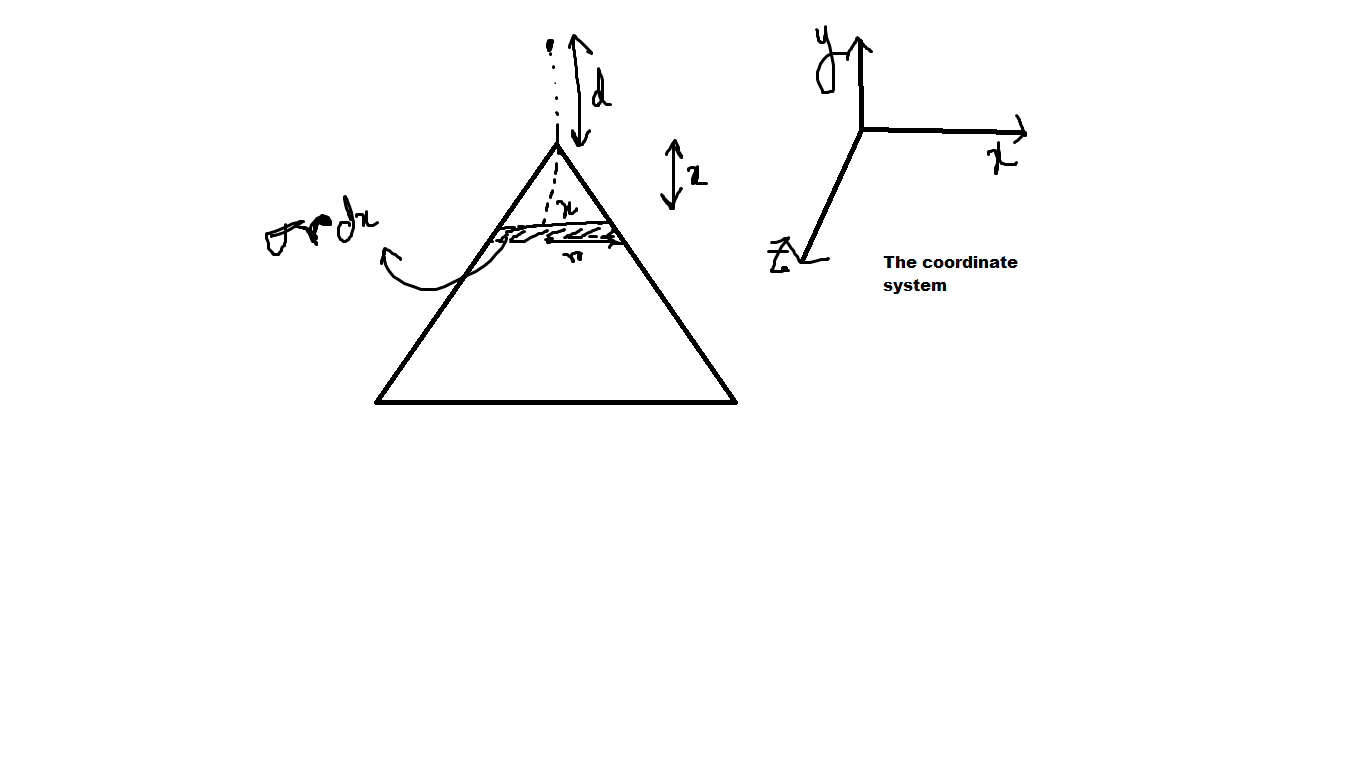
So By using Proportionality in triangle,

We get

$\dfrac{r}{x} = \dfrac{\dfrac{a}{2}}{\dfrac{\sqrt{3}a}{2}}$

$\implies r= \dfrac{x}{\sqrt{3}}$ .

Now for electric field, We have,

$dE \sin\theta = \dfrac{kd (dq)}{(x+d)^{\tiny \dfrac{3}{2}}}$

$E_{y} = \displaystyle{\int_{0}^{\sqrt{3}a/2} \dfrac{kd (dq)}{(x+d)^{\tiny \dfrac{3}{2}}}}$

We also know $dq= \sigma r dx$ .

After solving, we get $\displaystyle{\lim_{d \rightarrow 0} E(d)= 10.39}$ .

If I am wrong anywhere, Please help me correct it. Also the integral calculation can be a error.

Thanks for looking through my doubt.

Markdown

Appears as

*italics* or _italics_

italics

**bold** or __bold__

bold


- bulleted
- list

bulleted
list


1. numbered
2. list

numbered
list

Note: you must add a full line of space before and after lists for them to show up correctly

paragraph 1

paragraph 2

paragraph 1

paragraph 2

[example link](https://brilliant.org)

example link

> This is a quote

This is a quote

    # I indented these lines
    # 4 spaces, and now they show
    # up as a code block.

    print "hello world"

# I indented these lines
# 4 spaces, and now they show
# up as a code block.

print "hello world"

Math

Appears as

Remember to wrap math in $ ... $ or \[ ... \] to ensure proper formatting.

2 \times 3

2 \times 3

2^{34}

2^{34}

a_{i-1}

a_{i-1}

\frac{2}{3}

\frac{2}{3}

\sqrt{2}

\sqrt{2}

\sum_{i=1}^3

\sum_{i=1}^3

\sin \theta

\sin \theta

\boxed{123}

\boxed{123}

Easy Math Editor

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

@Steven Chase @Mark Hennings @Thomas Jacob @Aaron Jerry Ninan @Ranajay Medya @Spandan Senapati .

Please help me! I may have skipped some names. You can add them too!

Md Zuhair - 3 years, 2 months ago

I just solved it by integrating, with no simplifying tricks like the one given in the solution (ingenious as it is). I'll put up a solution in the next few days.

Steven Chase - 3 years, 2 months ago

That means my integral is correct, But the value isnt?

@Md Zuhair – I used an integral, but it wasn't necessarily your integral.

@Steven Chase – Ohkay, I see. I dont know why, I am not getting it. Did you just saw my solution. You can point out any mistake if you get there. else it may be fine.

@Md Zuhair – When calculating the contribution from one of the strips, you have to integrate as well. So the problem effectively boils down to a double integral. But I did the two integrations sequentially.

@Steven Chase – Okay, So I have to take a small element in that strip too?

@Md Zuhair – Yes. So integrating with infinitesimals within the strip gives you an expression for the contribution of a strip. Then integrating the contributions from the strips gives the final result. The first integral is readily done with an integral table. For the second integral, I used Wolfram Alpha. Then you have some interesting philosophizing to do regarding the limit of an arctangent before getting to the final answer.

@Steven Chase – Okay, Will try in that way! Thanks!

Thanks sir! Finally solved it using Integrals! But, Why do i need double integral here? Why cant i apply integral from the middle of the thin strip in the triangle?

@Md Zuhair – Did you do it by integrating the contributions from the strips?

@Steven Chase – Yes sir. Like the way you told

@Md Zuhair – Ok. And then it also takes an integral to figure out the contribution from a strip. That's why I refer to the whole process as effectively being a double integral.

Your way of writing fields due to an infinitismal element is wrong.Use a related result of finite length charged wire. $E=\frac {k\lambda }{d}(\sin \theta _{1}+\sin \theta _{2})$ along the radial direction and $\frac {k\lambda }{d}(\cos \theta _{1}-\cos \theta _{2})$ along the perpendicular. But if you want to develop your skills avoid integrals,symmetry helps a no of times,like considering hexagonal plates.

Spandan Senapati - 3 years, 2 months ago

I have a small qs. If does that $\dfrac{\sigma}{2 \epsilon_{0}}$ can be used for Any kind of plates? As i knew it is used for rectangular plates. Thanks

In this Q the concept of relative largeness plays a very important role. d->0 indirectly states that the point is near an infinitely large plane. I'll check if we can arrive at the same conclusion using the integration process.

Ranajay Medya - 3 years, 2 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$