Electric field and force

Can we solve this problem Anayltically
I will share my attempt within some hours.

#ElectricityAndMagnetism

This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.

When posting on Brilliant:

Use the emojis to react to an explanation, whether you're congratulating a job well done , or just really confused .
Ask specific questions about the challenge or the steps in somebody's explanation. Well-posed questions can add a lot to the discussion, but posting "I don't understand!" doesn't help anyone.
Try to contribute something new to the discussion, whether it is an extension, generalization or other idea related to the challenge.
Stay on topic — we're all here to learn more about math and science, not to hear about your favorite get-rich-quick scheme or current world events.

Markdown	Appears as
`italics` or `_italics_`	italics
`bold` or `__bold__`	bold
- bulleted - list	bulleted list
1. numbered 2. list	numbered list
Note: you must add a full line of space before and after lists for them to show up correctly
paragraph 1 paragraph 2	paragraph 1 paragraph 2
`[example link](https://brilliant.org)`	example link
`> This is a quote`	This is a quote
# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"	# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"

Math	Appears as
Remember to wrap math in `$` ... `$` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$

Comments

Is the answer:

$d_{max} = \frac{q(M+m)}{4 \pi \epsilon_o EL(M-m)}$

Karan Chatrath - 9 months ago

@Karan Chatrath No,but very very near to correct answer. I am not telling you answer because you always say, don't tell answer.

Talulah Riley - 9 months ago

Maybe I am missing something. Cannot spot my mistake.

Karan Chatrath - 9 months ago

@Karan Chatrath – @Karan Chatrath if you don't mind me, your answer is also incorrect with dimension.
By the way, do you like to see answer?

Talulah Riley - 9 months ago

@Talulah Riley – I think my answer is dimensionally correct. Please recheck this. Also, you may share the correct answer.

Karan Chatrath - 9 months ago

@Karan Chatrath – @Karan Chatrath OMG there is a coincidence if you watch answer basically the $L$ in your answer is managing the need of square root.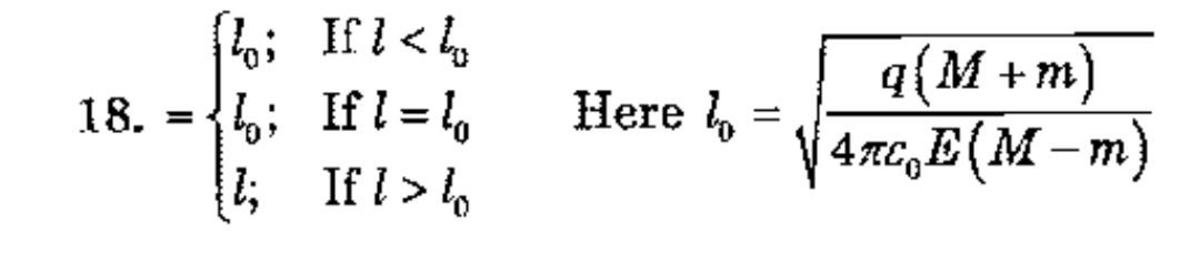
That's really sexy.

Talulah Riley - 9 months ago

@Talulah Riley – I think that the book is wrong here. I have done a numerical simulation and checked the expression that I got and the one in the book, and the one I have obtained seems correct. I even checked various possible cases by varying the initial separation parameter.

@Steven Chase could you validate this observation when possible?

Karan Chatrath - 9 months ago

@Karan Chatrath – I'm not even convinced that there is a maximum distance. I got the following results with the numerical values given in the code. It looks like the local maxima might just keep increasing.

import math

dt = 10.0**(-5.0)

q = 2.0
m = 3.0
M = 5.0
E = 7.0
L = 11.0
e0 = 1.0

k = 1.0/(4.0*math.pi*e0)

Dref = q*(M+m)/(4.0*math.pi*e0*E*L*(M-m))

#################################

t = 0.0
count = 0

xm = 0.0
xM = L

xmd = 0.0
xMd = 0.0

xmdd = 0.0
xMdd = 0.0

while t <= 200.0:

    xm = xm + xmd*dt
    xM = xM + xMd*dt

    xmd = xmd + xmdd*dt
    xMd = xMd + xMdd*dt

    D = xM - xm

    F = k*q*q/(D**2.0)

    Fm = q*E - F
    FM = q*E + F

    xmdd = Fm/m
    xMdd = FM/M

    t = t + dt
    count = count + 1

    if count % 1000 == 0:
        print t,D

Steven Chase - 9 months ago

@Steven Chase – I ran a quick simulation with your code and I see that the progressively increasing separation is a numerical issue that you seem to be having. If I use the explicit Euler solver, I get a result similar to yours. I am using a higher-order accurate integrator.

Karan Chatrath - 9 months ago

@Karan Chatrath – Yes, I neglected to check with multiple time steps and compare. When I run with a microsecond time step, the drift upwards is much smaller, but still there. It almost seems as if with a very small time step, the particle separation will oscillate between $L$ and zero in perpetuity.

Steven Chase - 9 months ago

@Steven Chase – I think it oscillates between $0.083$ and $L$ . This is the value I get with the expression and also validated using simulations. From the plots, it looks like zero as 0.083 is a relatively small magnitude.

Karan Chatrath - 9 months ago

@Karan Chatrath – So the max separation is $L$ for those numbers. But the expression doesn't reduce to $L$ , does it?

Steven Chase - 9 months ago

@Steven Chase – Indeed it does not. For the numbers you have chosen, the expression yields the minimum separation

Karan Chatrath - 9 months ago

@Karan Chatrath – I'm getting the impression that the qualitative behavior depends on the particular constants chosen.

Steven Chase - 9 months ago

@Steven Chase – Yes, initially, I just solved for the fixed points of $\dot{x}=f(x)$ and thought that my job is done. But when @Lil Doug shared the answer with me, showing the various cases, I realised that I had not thought it through. Having said that, I do think that the expression that the book shows is not correct.

Karan Chatrath - 9 months ago

@Steven Chase – I ran the simulation using the following parameters and got the result with matches with the expression that I derived. While testing with closed-form expressions, I like to use irrational numbers as parameters.

$q = \sqrt{2}$ $E = \sqrt{5}$ $L = \frac{\pi}{20}$ $m = \mathrm{e}$ $M = \mathrm{e}^2$ $\epsilon_o = 1$

Karan Chatrath - 9 months ago

@Talulah Riley – I look forward to seeing your attempt, after which I will share mine. Later, though.

Karan Chatrath - 9 months ago

@Steven Chase My attempt:

Coordinate of $M$ is $x_1$ and that of $m$ is $x_2$ .

Let:

$x = x_1 - x_2$

Applying Newton's second law gives:

$M\ddot{x}_1 = qE + \frac{Kq^2}{x^2}$ $m\ddot{x}_2 = qE - \frac{Kq^2}{x^2}$

Manipulating and rearranging both equations gives:

$\ddot{x}_1 - \ddot{x}_2 = \frac{Kq^2}{x^2}\left(\frac{1}{M} + \frac{1}{m}\right) + qE\left(\frac{1}{M} - \frac{1}{m}\right)$

$\implies \ddot{x} = A + \frac{B}{x^2}$

$A = qE\left(\frac{1}{M} - \frac{1}{m}\right)$ $B =Kq^2\left(\frac{1}{M} + \frac{1}{m}\right)$

$x(0) = L$ $\dot{x}(0) = 0$

$\ddot{x} = A + \frac{B}{x^2}$ $\implies \dot{x} d(\dot{x}) = \left(A + \frac{B}{x^2}\right) \ dx$

Integrating gives:

$\frac{\dot{x}^2}{2} = A + \frac{B}{x^2} + C$

Apply initial conditions and solve for integration constant $C$ . Finally, the separation is max or min when $\dot{x} = 0$ . Equating $\dot{x}=0$ gives a quadratic equations, one root of which is obviously $L$ . The other is:

$d = \frac{q(M+m)}{4 \pi \epsilon_o EL(M-m)}$

Whether $d$ is a max or min can be confirmed by a second derivative test, which gives rise to cases.

Karan Chatrath - 9 months ago

Does this method distinguish between local and global maxima?

Steven Chase - 9 months ago

Since we are solving a quadratic equation which has only two solutions, the local maxima and minima are actually the global maxima and minima.

Karan Chatrath - 9 months ago

@Karan Chatrath in the 3rd line of your solution it will be $m$

Talulah Riley - 9 months ago

Nice catch. Corrected now.

Karan Chatrath - 9 months ago

@Lil Doug Bro your problems are really hard. Lol.

Krishna Karthik - 9 months ago

Math	Appears as
Remember to wrap math in `\(` ... `\)` or `\[` ... `\]` to ensure proper formatting.
`2 \times 3`	$2 \times 3$
`2^{34}`	$2^{34}$
`a_{i-1}`	$a_{i-1}$
`\frac{2}{3}`	$\frac{2}{3}$
`\sqrt{2}`	$\sqrt{2}$
`\sum_{i=1}^3`	$\sum_{i=1}^3$
`\sin \theta`	$\sin \theta$
`\boxed{123}`	$\boxed{123}$