Electric Sandwich :: Try Open Physics Challenge !
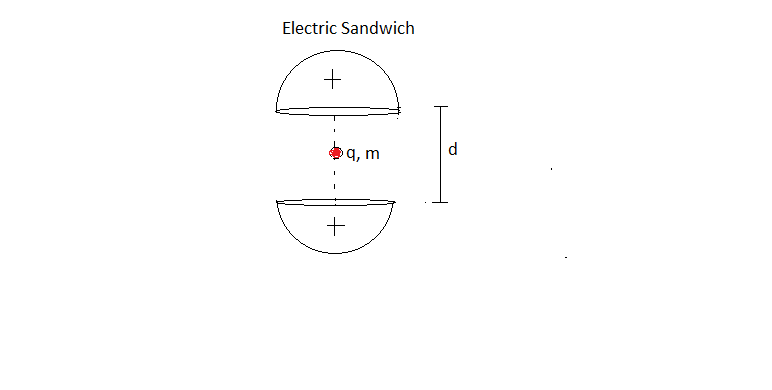
Given two identical Solid uniformly charged ( , ) hemisphere , initially system in equilibrium Find time period of small vertical oscillation of charged particle and mass .
Details :
*hemisphere are fixed
Take It as challenge , and try to solve it. And then Share your all approaches with us!
No vote yet
1 vote
Easy Math Editor
This discussion board is a place to discuss our Daily Challenges and the math and science related to those challenges. Explanations are more than just a solution — they should explain the steps and thinking strategies that you used to obtain the solution. Comments should further the discussion of math and science.
When posting on Brilliant:
*italics*or_italics_**bold**or__bold__paragraph 1
paragraph 2
[example link](https://brilliant.org)> This is a quote# I indented these lines # 4 spaces, and now they show # up as a code block. print "hello world"\(...\)or\[...\]to ensure proper formatting.2 \times 32^{34}a_{i-1}\frac{2}{3}\sqrt{2}\sum_{i=1}^3\sin \theta\boxed{123}Comments
We will proceed by finding the potential at the axis of a solid hemisphere at a distance of a from its center. We can do this by first finding potential due to a disk at it's axis and then integrating to get a sphere. I am simply giving formula here, and leaving the integration as an exercise to the reader.
V(a) is the potential at distance a when R=1 :
ϕ=2ε0ρV(a)=ϕ[3a2−3aa2+1−3aa2+1+3a1+21]
Now we know that the motion of this particle can be approximated to S.H.M. We will use the fact that total energy remains constant:
K.E of particle+ electrostatic P.E of particle= constant
⇒2mv2+qV(a+x)+qV(a−x)=K
Since R.H.S is constant w.r.t time, we will differentiate to get:
mvdtdv+qdxdV(a+x)×dtdx+qdxdV(a−x)×dtdx=0
⇒mdtdv=−qdxdV(a+x)−qdxdV(a−x)
We can now find the R.H.S of above equation by differentiating the V(a) function.
dxdV(a+x)=3ϕ[−2(a+x)2+1+(a+x)2(a+x)2+1−(a+x)21+2(a+x)]
In the above equation, we use the binomial approximation on each and every term (even the terms under the square root) and then neglect all terms where power of x is more than 1. I'm skipping the simplification, and giving the final answer at a=1:
dxdV(a+x)=3ϕ[1−2+2(8−52)x]
Hence: dxdV(a−x)=−3ϕ[1−2−2(8−52)x]
Therefore:
⇒mdtdv=−qdxdV(a+x)−qdxdV(a−x)=−3ϕ(8−52)qx
mdtdv=6ε0−ρq(8−52)qx
Finally, we have the expression of time period as:
2πρq(8−52)6mε0
Log in to reply
@Deepanshu Gupta @Mvs Saketh @Ronak Agarwal
Log in to reply
I will tell you what actually happened when I tried to solve this problem, I made the integral for electric field and in the integral itself I just added a little x with r and after series of approximations calculated the result.
But that doesn't seem elegant, hence I thought of differentiation method.
Log in to reply
That is acceptable, that is basically what you would do with differentiation as well,
as zero order term of field is 0 (since it is equillibrium point), and 1st order is dominant and restoring, and finally second order and higher orders are neglected. So, approximation here is just as rigorious as differentiation
@Raghav Vaidyanathan - nice, atleast you confirmed the answer, and yours seems simpler though there are some complex derivatives to be done, and maybe we should expect it to be bit complicated since this is not some mathematically simple problem anyway :)
Okay. I actually found a lot of similarity between the method above and yours. After posting this, I tried using Newton-Leibniz rule in order to calculate the derivative of V(a) directly instead of getting V(a) and then differentiating. It does work. But I'm quite unsatisfied with the fact that this problem takes a while to solve, no matter what method one uses.
Nice Raghav ! Now I realise finding field alway's is not good idea ... atleast for me , who know's very li'l calculus ..! You did it nicely bro ! Thanks for sharing !
Firstly I am using a simple result that, electric field due to a disc of radius r having a surface charge density σ at on point on the axis at a distance z from the centre of the disc is given by :
E=2ε0σ(1−z2+r2z)
In my diagram I have taken a angular elemental disc whose radius is Rsin(θ) and width of disc is given by =Rsin(θ)dθ, also to note that here σ=ρ×(Width)
Now electric field due to that element at a point that is at a distance r from the centre of the hemisphere is given by :
dE=2ε0ρRsinθ(1−(r+Rcosθ)2+(Rsinθ)2(r+Rcosθ))dθ
Integrating it our we have :
E(r)=2ε0ρR∫0π/2(sinθ−(r+Rcosθ)2+(Rsinθ)2(r+Rcosθ)sinθ)dθ
Now we know that for small x we have :
E(r+x)=E(r)+xE′(r)
and
E(r−x)=E(r)−xE′(r)
We have net electric field due to both hemisphere's when particle is at a distance x from it's mean position is given by :
E=−2xE′(r)
Now by newton leibnitz rule we have :
E′(r)=2ε0ρ∫0π/2(((r+Rcosθ)2+(Rsinθ)2)3/2R3sin3θ)dθ
Evaluting the derivative at R , (since the mean position is at a distance R from the centre of the two hemispheres.)
E′(R)=2ε0ρ∫0π/2(sin32θ)dθ=12ε0ρ(8−52)
Hence acceleration of the particle is given by :
a=−6mε0ρq(8−52)x
Hence the time period is given by :
T=2πρq(8−52)6mε0
I have jumped many steps it seems hence if you have any confusion ask in the comments.
Log in to reply
i see you have not used wolfram, Nice +1
Log in to reply
did you solved it ? @Mvs Saketh
Log in to reply
i got to the expression of field for hemisphere and then thought it can be solved so i stopped
Log in to reply
Please post how much you reach .... Ronak and me discuss this earliear that this is very difficult to solve , if we use conventional method ... Roonak approach is very cool ! That's why I posted this as a note !
Log in to reply
My approach is no different from Ronaks, i too use Newton Leibinz method to avoid Dauting Integrals or wolfram where needed, i dont think i have anything more to add to him , But i shall add if i do get some idea :)
Log in to reply
Please Tell what should we do after this ? Please suggest , if want to do in different manner as Ronak awesomely did,....
E(r)=2ερ∫02πcosθ−(r)2+1+2rcosθ(r+sinθ)cosθdθ
I had puted the value R=1 .
Log in to reply
Well, you can use WolfRam, though i know not if it can do it,
But,i dont think i can solve it, (not in a simple manner surely)
Log in to reply
I think there is an easier way to do this problem rather than finding field. Why not find potential energy? Then we can use total energy equation and differentiate it to get SHM equation.
I think there is an easier way to do this problem rather than finding field. Why not find potential energy? Then we can use total energy equation and differentiate it to get SHM equation.
Log in to reply
Have you done it with that ....?
yes you can, but whether it is really easy is not has to be tried, we do not yet know if the integral for potential of hemisphere is simpler (though it usually is the case that potential is simpler than field) (have you tried that?)
Log in to reply
It is simpler, but I think I am going wrong in some the integration somewhere. I don't think I'm getting the boundary conditions right when I substitute them in my equation
Log in to reply
You can post important expression here ..... The purpose of this note is exatly that ... to discuss various Possiblities ! @Raghav Vaidyanathan Please post what'sever you get ... may be we together complete it ... You can skips unnecceserry steps for posting here to save ur time ..!
Yes @Mvs Saketh @Deepanshu Gupta @Ronak Agarwal
I have tried it using the potential method and have gotten the right answer. I will post an overview soon.
Log in to reply
we are waiting !
I think , u are decide to not to reply me ... am i right ? :) ... I have recently mentioned you 2-3 times but you are not responding ...
Log in to reply
Woah bro, Chill not at all, i was solving your cylinder problem and hence did not reply ,
Also, i do not get notifications if some one mentions me ,
Log in to reply
mention and disput's are are comes on Emails only ... But okay leave that , I actually replied to your comment on My problem Fearless boy..... and where I asked something please reply there ...!